Hands On ML

핸즈온 머신러닝 영어 PDF를 읽고 공부하면서 내용을 정리하고 있다. 정리에 나온 대부분의 코드와 이미지들은 해당 PDF에서 가져왔다.

Chapter 5 - Support Vector Machines

서포트 벡터 머신(Support Vector Machine)은 linear 혹은 nonlinear 분류, 회귀, outlier detection을 하는데 사용할 수 있는 강력한 ML 모델 중 하나이다. 복잡하지만 크기가 작은 dataset에도 잘 작동하는 장점이 있다.

5.1 Linear SVM Classification

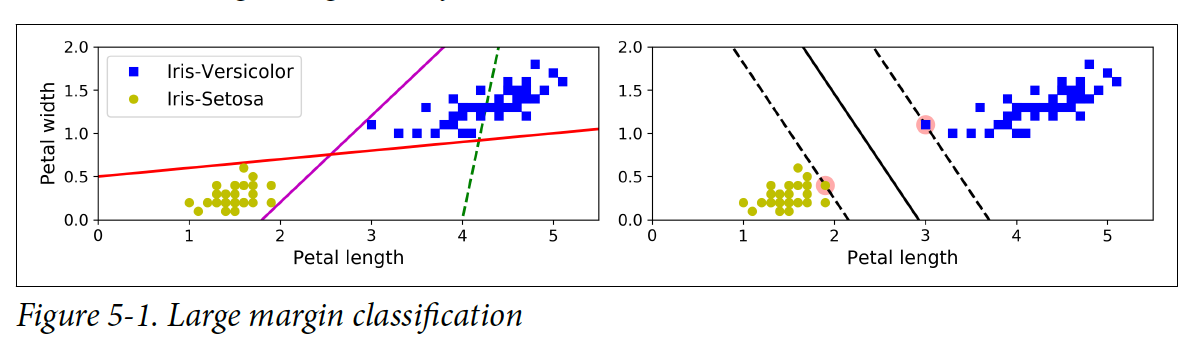
왼쪽 그림에 있는 linear 모델들은 클래스들을 어느정도 분류를 하지만, decision boundary가 training set의 인스턴스들과 가깝기 때문에 새로운 인스턴스에는 잘 작동하지 않을 가능성이 높다. 반면에, 오른쪽 그림에 있는 모델은 SVM이고 클래스들로부터 decision boundary가 멀리 떨어져있을 뿐더러 training set의 인스턴스와 가능한 먼 거리에 있다. 그림에서 parallel하게 이뤄진 점선을 street이라고 부르고 최대한 서로가 멀리 떨어져 있게 모델을 fit하려고 한다. 이러한 분류를 large margin classification이라고 부른다.

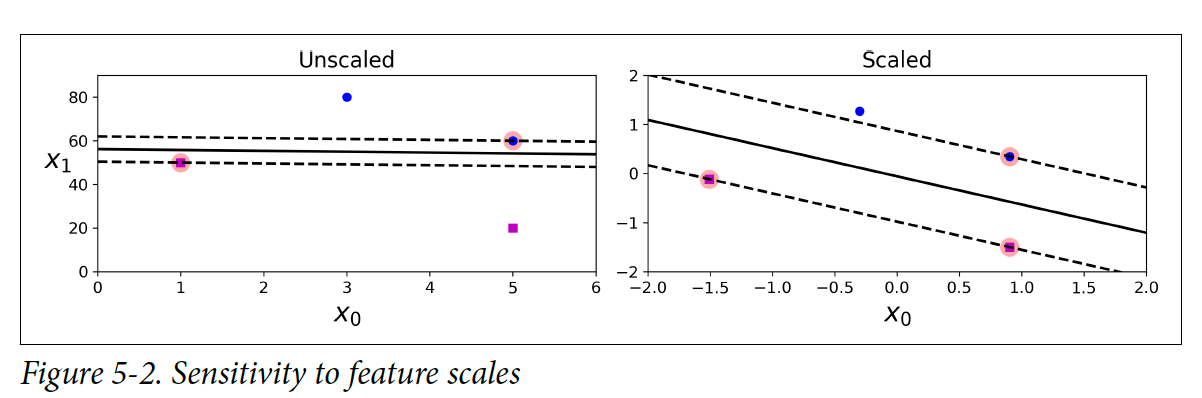
** 다만, SVM은 특징점(feature)들에 스케일에 민감하다. 밑에 그림을 보면 같은 스케일로 특징점(feature)들을 변환했을 때 인스턴스간 더 멀리 떨어져서 decision boundary를 형성한 것을 볼 수 있다. 이러한 특징 때문에, SVM을 사용하려면 특징점(feature)들을 스케일링(e.g. Scikit-Learn의 StandardScaler)해야 한다.

Soft Margin Classification

위에서 처럼 다른 클래스들을 나눌 때 인스턴스들로부터 가능하면 멀리 decision boundary를 형성하는 것을 hard margin classification이라고 부른다. 이 분류는 2가지 이슈가 있다. 하나는, 데이터가 직선으로 나눌 수 있을 때만 제대로 작동한다는 것이고, 다른 하나는, outlier들에 민감하다는 것이다.

밑에 왼쪽 그림에 극단적인 outlier를 하나를 추가하니 hard margin classificaiton으로는 분류를 할 수 없게 되었다. 오른쪽에는 다른 클래스에 매우 근접한 outlier를 추가하니, decision boundary가 매우 좁아지게 되었고 새로운 데이터가 들어올 때 일반화를 하기 힘들게 되었다.

이러한 문제들을 방지하기 위해서는 조금 더 유연한 모델을 사용해야 한다. Soft margin classification은 street(parallel한 점선들)을 최대한 멀리 있게 유지하고 margin violations(i.e. street 중간에 혹은 다른 사이드에 있는 인스턴스들)들을 제한하는 것이 목표이다.

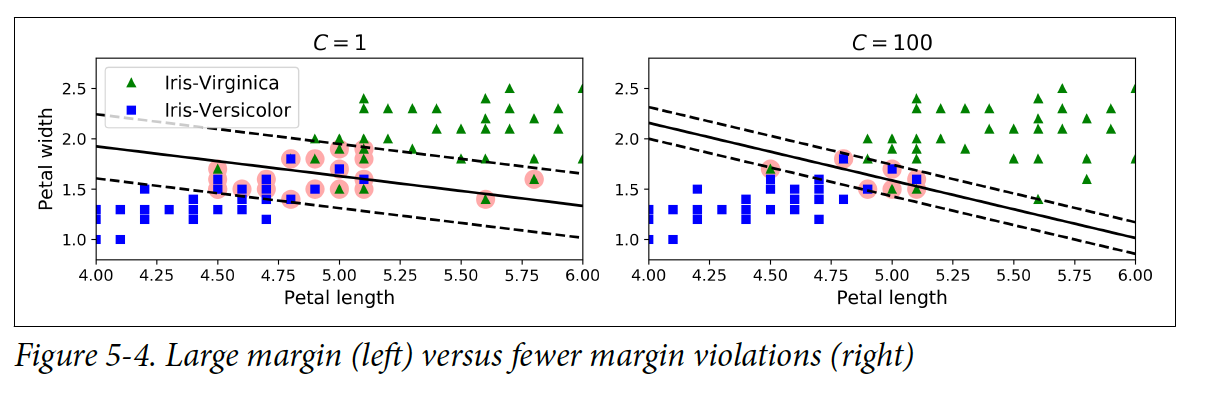
Scikit-Learn의 SVM 클래스에서는 C 하이퍼파라미터를 조절할 수 있다: 값이 작으면 street는 더 넓어지지만 margin violation은 증가한다. 밑에 왼쪽 그림 같은 경우는 C 값이 낮기 때문에 street은 넓고 margin violation은 많다. 반면에 밑에 오른쪽 그림은 C의 값이 크기 때문에 street가 좁지만 margin violation의 수도 매우 적다.

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris = datasets.load_iris()
X = iris["data"][:, (2,3)] # petal의 길이, petal의 넓이
y = (iris["target"] == 2).astype(np.float64) # Iris-Virginica

svm_clf = Pipeline([
    ("scaler", StandardScaler()),
    ("linear_svc", LinearSVC(C=1, loss="hinge")),
])

svm_clf.fit(X,y)

print(svm_clf.predict([[5.5, 1.7]])
# array([1.])

Logistic Regression 분류기와는 달리 SVM 분류기는 각 클래스에 대해 확률을 제공하지 않는다. LinearSVC 말고 SVC(kernel="linear",C1)을 사용해도 되지만 데이터셋이 크면 속도가 매우 느리기 때문체 추천은 하지 않는다. 다른 대안으로는 SGDClassifier(loss="hinge", alpha=1/(m*C))를 사용하는 것이다. 이 방법은 LinearSVC보다 수렴은 느리게 하지만 메모리에 다 들어가지 않는 큰 데이터셋을 다룰 때는 유용하게 사용할 수 있다.

5.2 Nonlinear SVM Classification

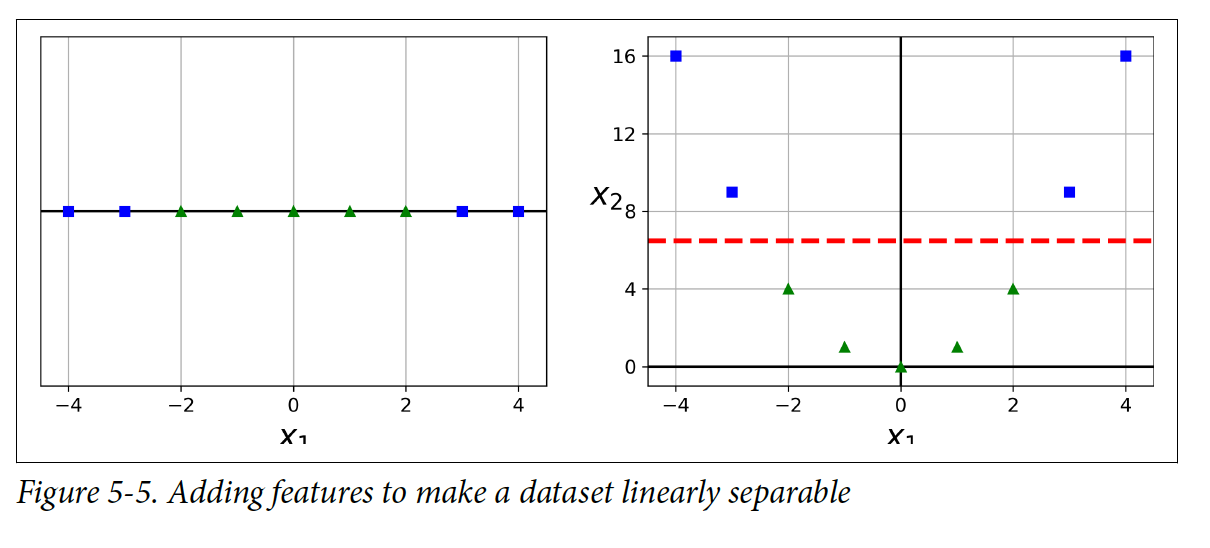
많은 데이터셋들은 직선으로 분류가 되지 않는 경우가 많다. 이러한 경우에는 feature(특징점)들을 추가해서 직선으로 분류가 가능하게 만들면 된다. 밑에 그림 같은 경우에 feature(특징점)이 하나일 떄는 직선 하나로 분류할 수가 없었는데 feature(특징점)을 하나 추가한 이후에 분류가 가능해졌다.

이 아이디어를 구현하려면 PolynomialFeatures transformer, StandardScaler, LinearSVC를 포함한 Pipeline을 만들어야 한다.

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

poly_svm_clf = Pipeline([
    ("poly_features", PolynomialFeatures(degree=3)),
    ("scaler", StandardScaler()),
    ("svm_clf", LinearSVC(C=10, loss="hinge"))
])

poly_svm_clf.fit(X,y)

Polynomial Kernel

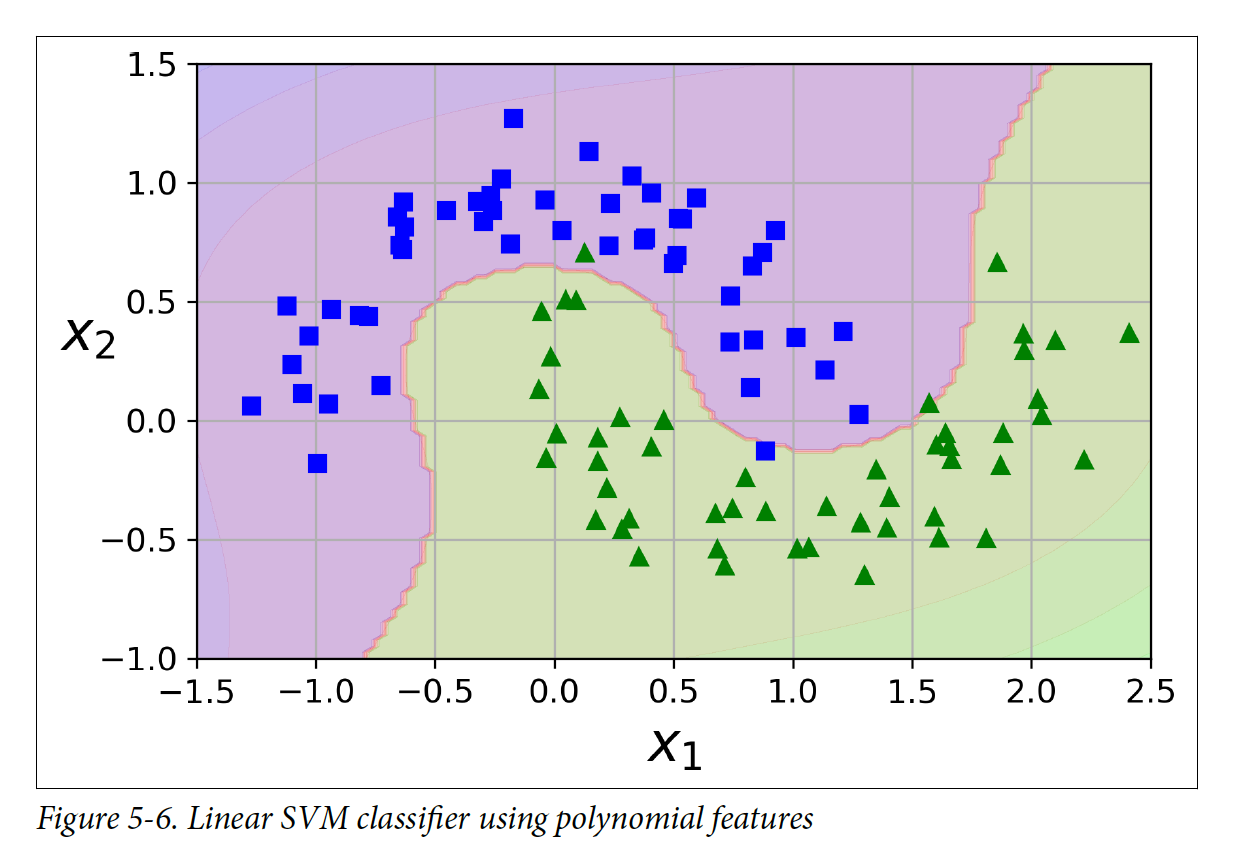
Polynomial degree를 추가하면 복잡한 dataset에 더 잘 fit하게 만들 수 있지만, 모델이 너무 느려진다. SVM은 높은 polynomial degree를 추가하면서도 모델이 느려지지 않도록 **kernel trick** 이라는 것을 제공한다. 실제로 polynomical feature(특징점)들을 추가하지는 않지만 추가하는 것과 같은 결과가 나오게 한다.

밑에 코드에서 SVM 분류기가 3 degree를 가진 polynomial kernel을 사용해서 학습을 한다. Polynomial degree가 높아지면 overfitting(오버피팅)이 발생한다.

from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
    ("scaler", StandardScaler()),
    ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
])

poly_kernel_svm_clf.fit(X,y)

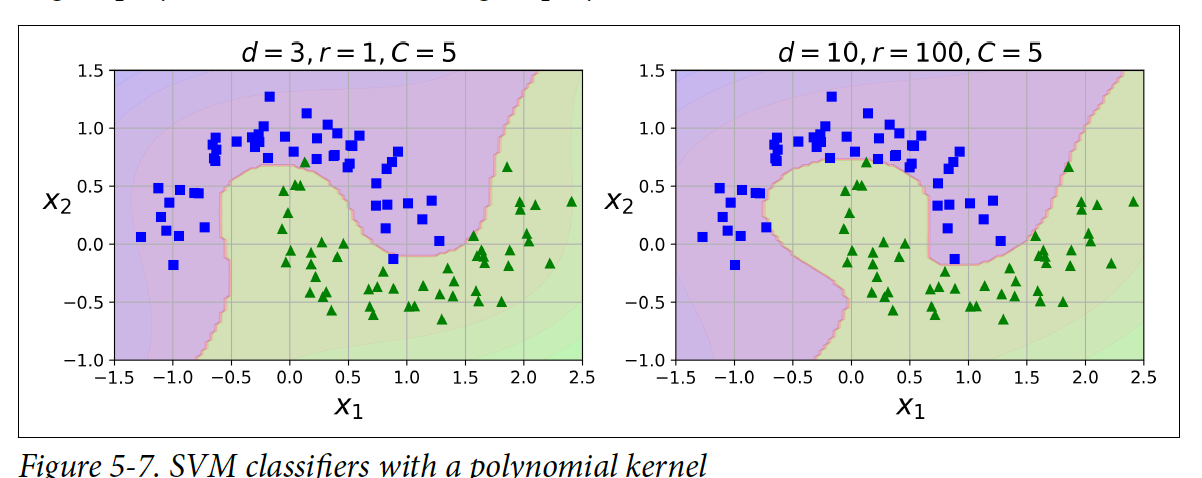
Adding Similarity Features

Nonlinear 문제를 해결하는 다른 방법은 similarity function을 사용해서 feature(특징점)들을 추가하고 인스턴스들이 특정한 landmark와 얼마나 유사한지 측정하는 것이다.

1-D 데이터셋에 2개의 landmark들을 추가해보자: x1 = -2, x1 = 1. 그 다음에 similarity function을 Gaussian Radial Basis Function(RBF)로 설정을 해보자 r=0.3

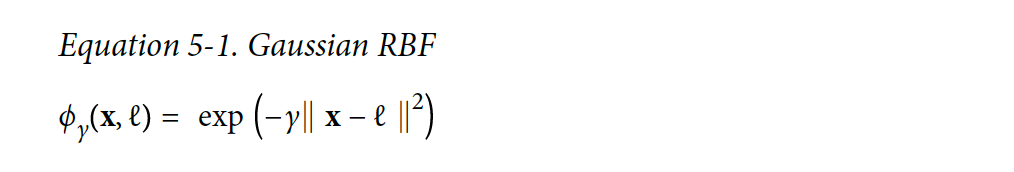
위 식은 0(landmark에서 떨어짐)~1(landmark와 가까움) 범위의 벨처럼 생긴 함수이다. 왼쪽 밑에 그림을 보면, x1 =-1일 때 첫 번째 landmark에서 1 만큼 떨어져 있고 두 번째 landmark에서 2만큼 떨어져 있다. 새로운 특징점(feature)는 x2 = exp(-0.3 x 1^2) = 0.74 이고 x3 = exp(-0.3 x 2^2) = 0.30이다. 오른쪽 밑에 그림은 transform된 데이터 셋을 보여주고 이제는 직선으로 분류가 된다.

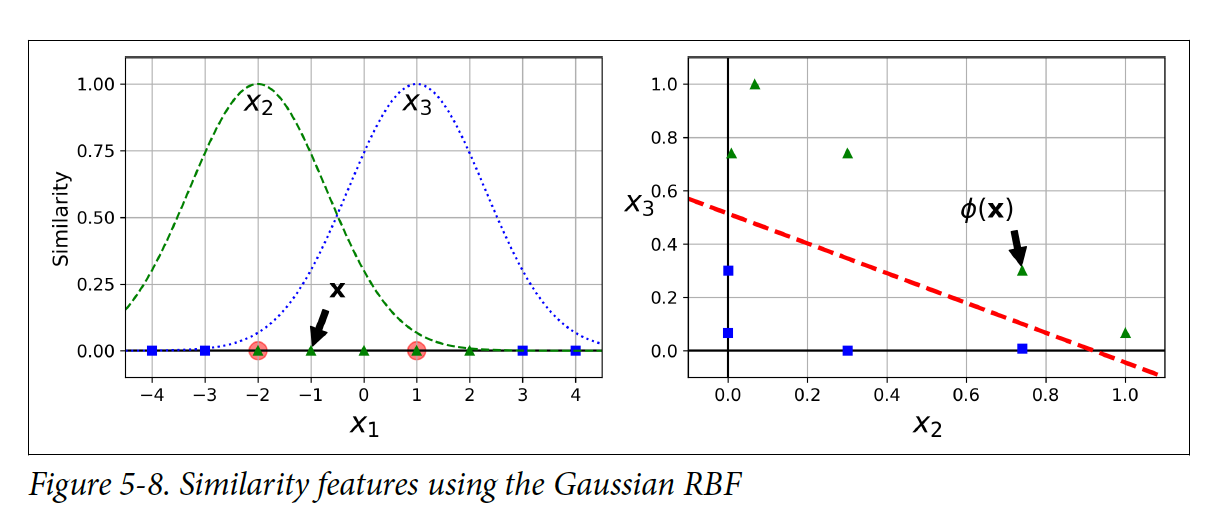
그렇다면 landmark는 어떻게 선택해야하는지에 대한 궁금증이 생길 것이다. 가장 간단한 방법은, 데이터셋의 각 인스턴스 위치에 landmark를 만드는 것이다. 이러한 방법으로 차원을 많이 만들 수 있고 transform된 training set이 직선으로 분류가 될 가능성이 높아진다. 이 방법의 단점은 training set이 매우 크면, feature(특징점)들의 수도 매우 많아진다는 것이다.

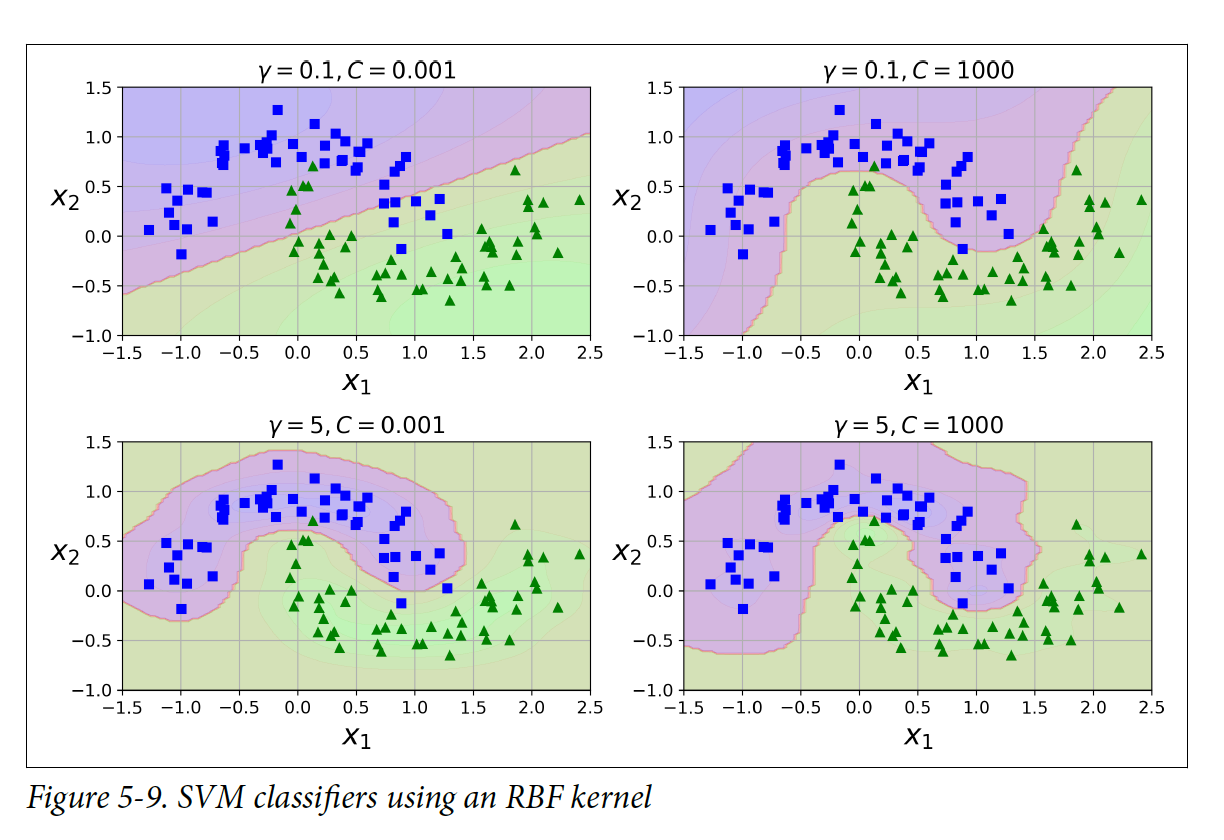
Gaussian RBF Kernel

Similarity function 방법은 연산이 많아지기 때문에 모델을 학습하는데 오래 걸리게 된다. 여기서 다시 kernel trick을 사용할 수 있다.

rbf_kernel_svm_clf = Pipeline([
    ("scaler", StandardScaler()),
    ("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
])

rbf_kernel_svm_clf.fit(X,y)

코드에서 gamma값을 증가시키면 벨 모양이 더 좁아지게 되고 decision boundary가 더 불규칙적으로 변하게 된다. 그렇기 떄문에 모델이 오버피팅을 하면 gamma값을 줄여야 하고, 언더피팅을 하면 증가시켜야 한다(C 하이퍼파라미터와 비슷하다)

Computational Complexity

LinearSVC 클래스는 kernel trick을 제공하지는 않지만, training 인스턴스와 수와 feature들의 수에 linear하게 스케일한다. 그래서 시간 복잡도는 O(m x n)이다. 높은 정확도가 요구 될 떄는 알고리즘을 학습하는데 더 오래 걸린다.

SVC 클래스는 kernel trick을 제공한다. 이 알고리즘의 시간 복잡도는 평균적으로 O(m^2 x n) ~ O(m^3 x n)이다. Training 인스턴스가 많아지면 시간이 매우 오래 걸린다는 의미이다. 복잡하지만 training set이 작은 데이터 셋의 경우에는 적합하다.

5.3 SVM Regression

SVM Regression은 위에서 언급되었던 linear & nonlinear classification과는 달리 margin violation들을 제한하면서 가능하면 많은 인스턴스들을 street에 담으려고 한다. Street의 너비는 ϵ 하이퍼파라미터로 조절이 가능하다.

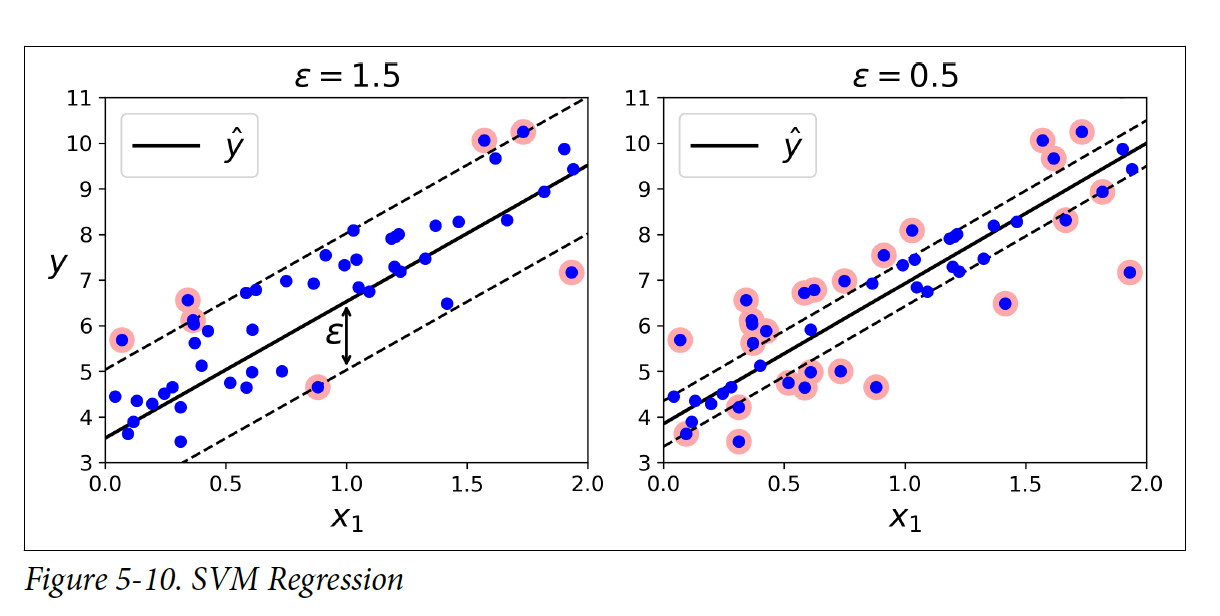
Scikit-Learn의 LinearSVR 클래스를 사용해서 SVM Regression을 구현할 수 있다.

from sklearn.svm import LinearSVR, SVR

svm_reg = LinearSVR(epsilon=1.5)
svm_reg.fit(X,y)

svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1)
svm_poly_reg.fit(X,y)

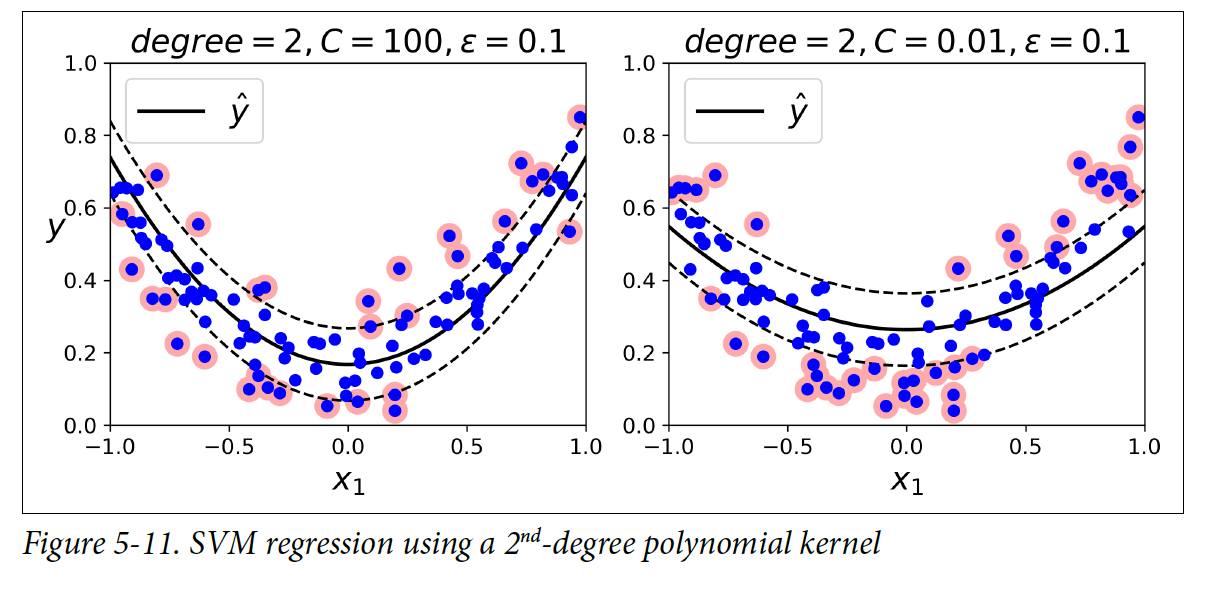
Nonlinear regression에도 해당 클래스를 사용할 수 있다. Polynomial kernel을 사용해서 복잡한 모델에도 적합할 수 있게 regression 모델을 만들 수 있다. 또한, C의 값에 따라서 정규화의 정도를 조절할 수 있다. C 값이 높으면 정규화가 덜 되고, 값이 낮으면 정규화가 더 된다.

SVR 클래스는 SVC와 유사하고, LinearSVR 클래스는 LinearSVC클래스와 유사하다.

5.4 Under the Hood

이 섹션에서는 SVM이 실제로 어떻게 예측을 하고 어떻게 알고리즘을 학습하는지 설명할 예정이다. 이번 섹션에서는 bias term을 지칭할 때 단순하게 b로, feature weights vector는 w로 나타낼 것이다.

Decision Function and Predictions

SVM은 새로운 인스턴스를 decision 함수에 넣어서 예측을 한다.

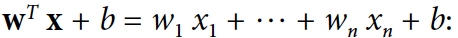
해당 함수의 값이 positive면 예측된 클래스 y_hat을 positive 클래스(1)로 분류하고 그렇지 않다면 negative 클래스(0)으로 분류한다.

SVM을 학습한다는 것은 margin violation을 피하면서 margin을 가능한 넓게 만드는 w와 b의 값을 찾는 것을 의미한다.

Training Objective

Weight 벡터 w가 작을수록 margin은 커진다. 우리의 목표는 ∥w∥ 값을 최소화해서 큰 margin을 얻는 것이다.

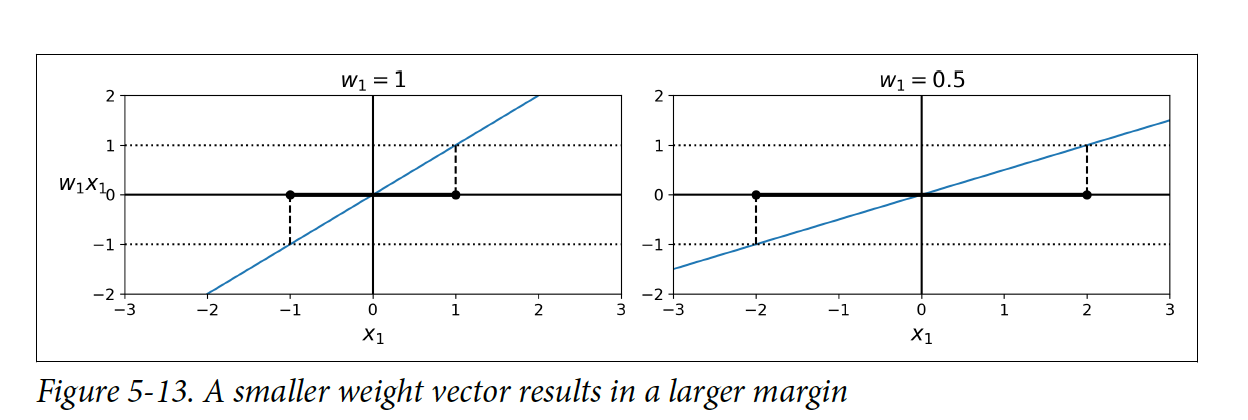
그러면서도 margin violation을 피해야 하기 떄문에 decision 함수는 모든 positive training 인스턴스에 대해 1보다 커야 하고, negative 인스턴스에 대해서는 -1 보다 작아야 한다. t(i) = –1을 negative 인스턴스로 정의하고, t(i) = 1을 positive 인스턴스로 정의했을 때, 모든 인스턴스에 대해서 다음과 같이 정의할 수 있다:

Hard margin linear SVM 분류기의 목표는 다음과 같아진다.

여기서 1/2를 사용한 이유는 1/2∥w∥^2가 미분하기 더 간편하기 때문이다.

Soft margin의 목표를 얻기 위해서는 slack variable ζ(i) ≥ 0이라는 것을 각 인스턴스에 적용해야 한다. ζ(i)에서 i의 의미는 i 번째 인스턴스가 얼마나 margin을 violate할 수 있는지이다. 이제 2가지의 목표가 부딪히게 된다: margin violation을 줄이기 위해 slack variable을 가능하면 작게 만드는 것과, margin을 증가시키기 위해 1/2wTw를 가능한 작게 만드는 것. 여기에 C 하이퍼파라미터의 존재가 필요하게 된다.

** 이 섹션에 추가적인 내용들이 있지만, ML을 시작한지 얼마 되지 않았기에 이해가 되지 않아서 나중에 더 공부 후에 업데이트 하려고 한다.