Hands On ML

핸즈온 머신러닝 영어 PDF를 읽고 공부하면서 내용을 정리하고 있다. 정리에 나온 대부분의 코드와 이미지들은 해당 PDF에서 가져왔다.

Chapter 4 - Training Models

이번 섹션에서는 Linear regression model의 2가지 학습방법을 알아볼 예정이다:

“closed-form” 방정식을 사용해서 training set에 가장 잘 fit하는 parameter를 계산 (i.e., cost 함수를 최소화 해주는 모델 parameter)
Gradient Descent 사용하기. 점진적으로 model parameter를 수정해서 training set에 대한 cost 함수 최소화.

그 다음에는 Polynomial Regression을 살펴보면서 nonlinear dataset을 fit하는 모델을 알아볼 것이다. 하지만, 해당 모델은 Linear Regression보다 parameter의 수가 많기 때문에 trainig data에 overfitting할 가능성이 높다.

4.1 Linear Regression

일반적으로, linear model은 입력의 가중치 합(weighted sum)과 bias term(or intercept term)을 계산해서 예측을 한다.

Linear Regression model prediction

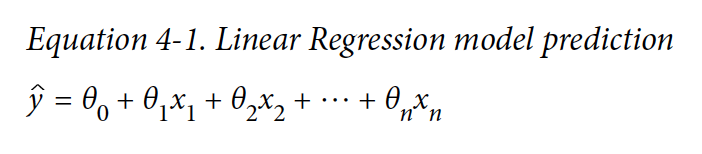
y_hat - 예측된 값
n - 특징(feature)들의 수
x_i - i 번째 feature 값
θ_j - j 번째 모델 파라미터 (θ_0 은 bias term이다)

해당 식은 벡터화 형식(vectorized form)을 사용해서 더 간결하게 쓸 수 있다.

θ - model의 파라미터 벡터이다. bias term과 θ_1~θ_n 특징들의 가중치(feature weight)들을 포함한다
x - 인스턴스의 특징 벡터(feature vector)이다. x_0 ~ x_n을 포함하고 있고, x_0은 항상 1이다.
θ . x - 벡터 θ와 x의 dot product이다. (θ_0x_0+…θ_nx_n)
h_θ - hypothesis 함수이고 θ 를 모델 파라미터로 사용한다.

위에 식이 Linear Regression 모델을 나타낸다. 그렇다면 이제 이 모델을 학습시켜야 된다. 학습이라함은 파라미터를 조정해서 모델이 training set에 가장 잘 fit하게 만드는 것을 의미한다. 회귀 모델에서 가장 일반적으로 사용되는 성능측정 방법은 RMSE(Root Mean Square Error)를 사용하는 것이다. Linear Regression을 학습하려면 RMSE값을 최소화하는 θ값을 찾아야 한다.

실제로는 MSE(Mean Square Error)를 최소화하는 것이 RMSE보다 더 간단하고, 결과도 같다.

MSE cost function for Linear Regression model

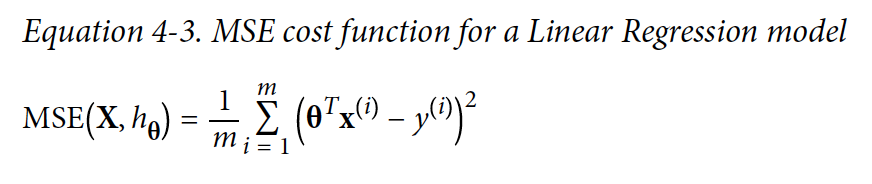
4.1.1 Normal Equation

Cost 함수를 최소화하는 θ 값을 찾기 위해서 Normal Equation을 사용할 수 있다.

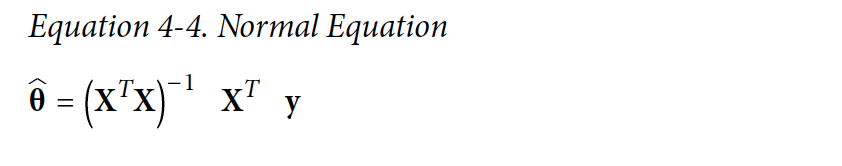
θ_hat - cost 함수를 최소화하는 θ의 값
y - y(1) ~y(m)을 포함하는 벡터의 target 값

4.1.2 Linear Regression 생성

import numpy as np
X = 2 * np.random.rand(100,1)
y = 4 + 3 * X + np.random.randn(100,1)

np.random을 사용해서 랜덤한 dataset을 만들었다.

θ_hat을 normal equation으로 구하려면 위에 식처럼 X를 전치한 값과 X의 내적을 구하고 그 행렬의 가역행렬을 구해야 한다. 그러고 나서 구해진 값과 전치 X의 내적을 구한 다음에, 다시 그 값과 y의 내적을 구하면 θ_hat을 구할 수 있게 된다. numpy의 np.linalg 모듈의inv() 함수를 사용해서 행렬의 가역행렬을 계산하고 dot() method를 사용해서 내적을 할 수 있고, 코드는 다음과 같다:

X_b = np.c_[np.ones((100,1)), X] # x0=1 각 인스턴스에 더해준다
theata_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)

theta_best
# array([[4.215xxx], [2.77xxx]])

위처럼 normal equation식에 값들을 대입해서 θ_hat을 구하는 방법도 있지만, scikit-Learn으로 linear regression을 사용해서 더 간단하게 구할 수 있다.

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)
lin_reg.intercept_, lin_reg.coef_
# (array([4.215xxx]), array([2.770xxx]))

lin_reg.predict(X_new)
# array([[4.215xx], [9.755xxx]])

Linear Regression 클래스는 scipy.linalg.lstsq 함수에 기반해 있어서 직접 호출이 가능하다:

theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
theta_best_svd
# array([[4.215xxx], [2.770xxx]])

해당 함수는 X의 pseudoinverse(Moore-Penrose inverse)를 계산한다. Pseudoinverse는 특이값 분해라고 불리는 Singular Value Decomposition(SVD)를 사용한다. Training set X를 U Σ V^T로 분해한다. Σ+ 행렬을 계산하기 위해서 tiny threshold 값보다 작은 모든 값들을 0으로 설정하고, 0이 아닌 값들을 inverse로 대체한다, 그러고 나서 결과로 나온 행렬을 전치한다. 이 방법은 Normal Equation을 계산하는 것보다 더 효율적이다. Normal Equation 같은 경우에 X^TX가 역행렬이 안될 때 작동하지 않는다.

(SVD의 더 자세한 내용은 블로그 참고)

4.1.3 Computational Complexity

Normal Equation은 연산 복잡도는 O(n^2.4) ~ O(n^3)이다.

반면에 Linear Regression이 사용하는 SVD는 O(n^2)이다.

4.2 Gradient Descent

경사 하강법(Gradient Descent)은 처음에 θ를 랜덤 값으로 초기화한 다음에, 점진적으로 cost 함수를(e.g. MSE) 줄여서 최소점으로 수렴한다. Gradient가 하강하는 방향으로 점진적으로 가고 0이 되면 최소점에 도달하게 된 것이다.

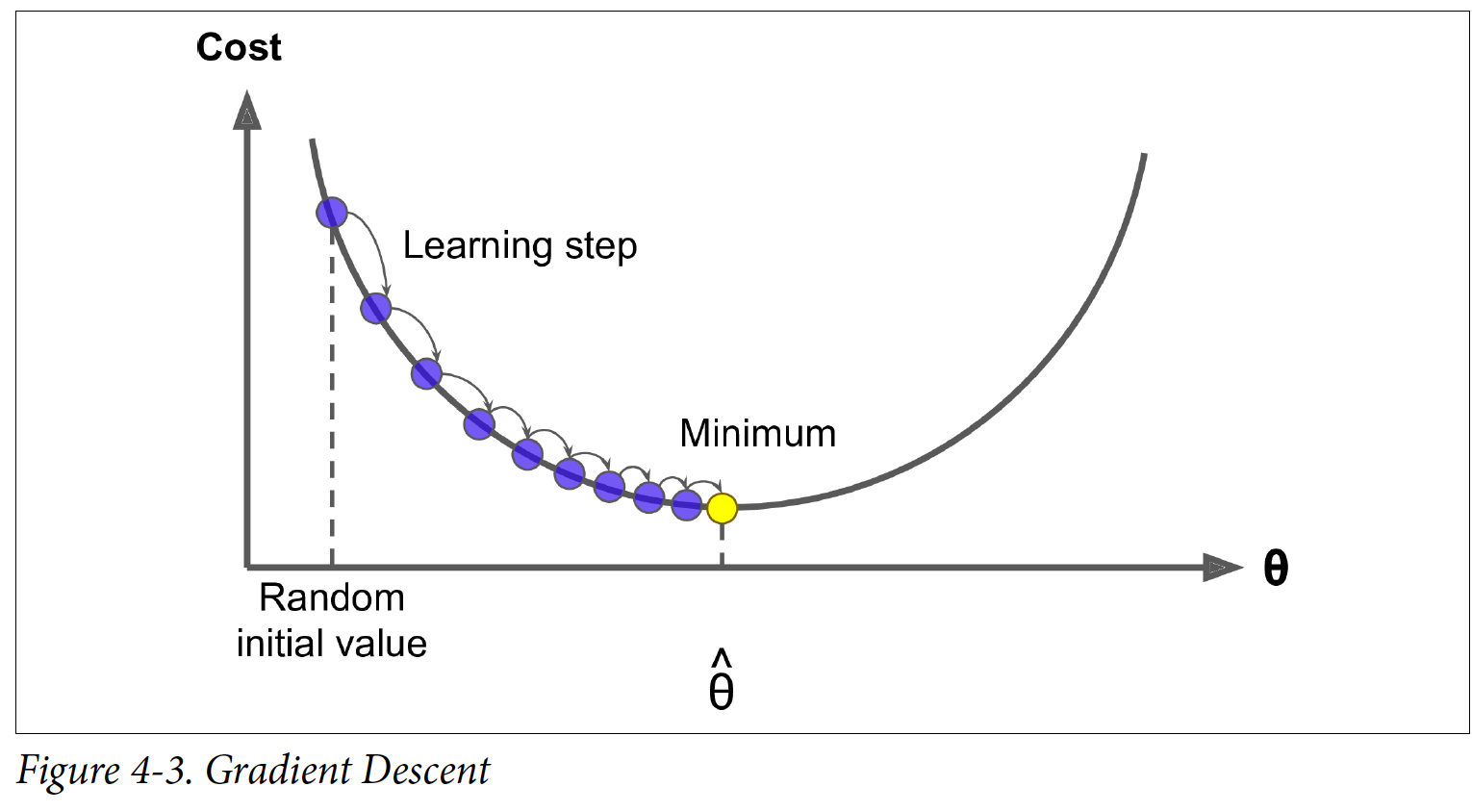
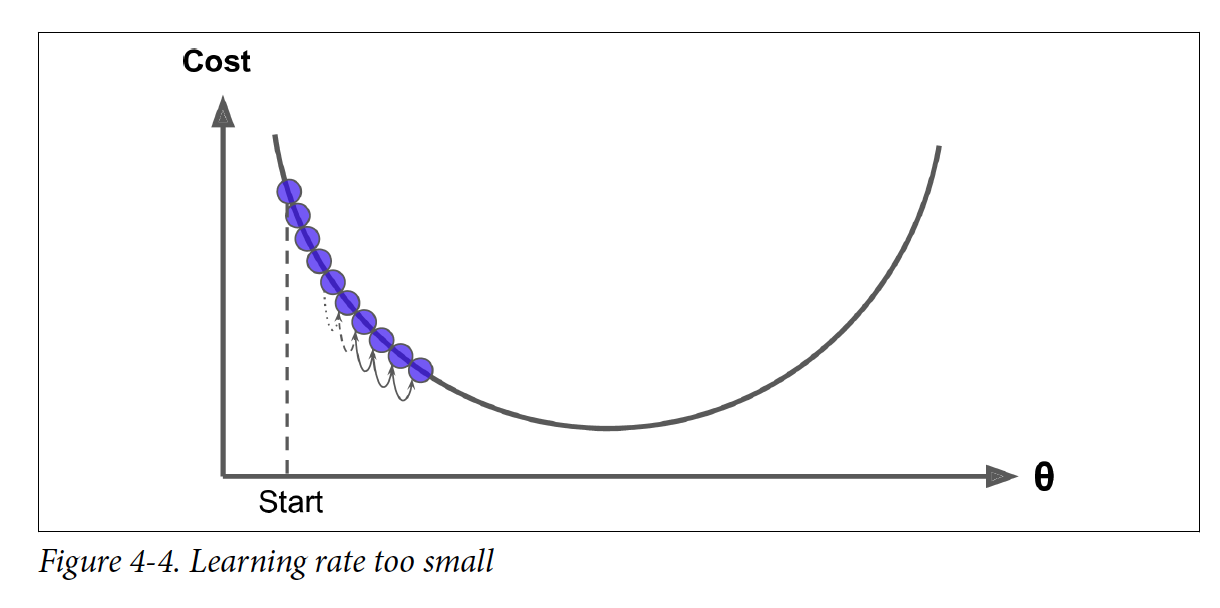
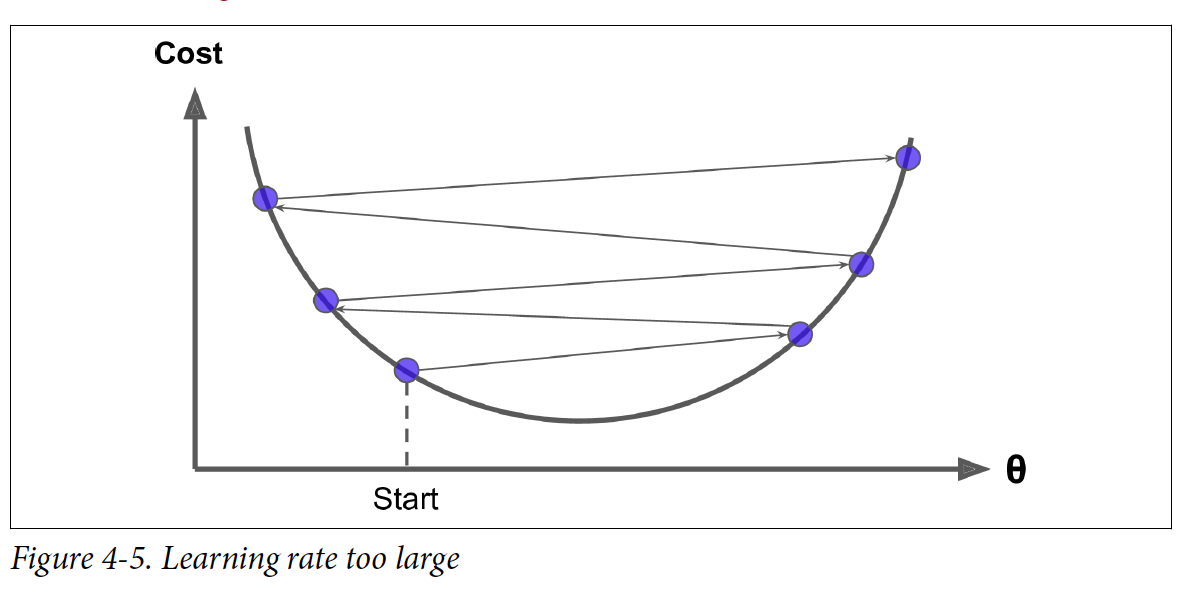
경사 하강법(Gradient Descent)에서 중요한 파라미터는 Step의 size이고 이는 learning rate라는 hyperparameter로 정해진다. Learning rate가 너무 작으면 iteration 수가 많아지고 시간도 오래 걸리게 된다. 반면에 learning rate가 너무 크면 제대로 수렴하지 않을 수 있다.

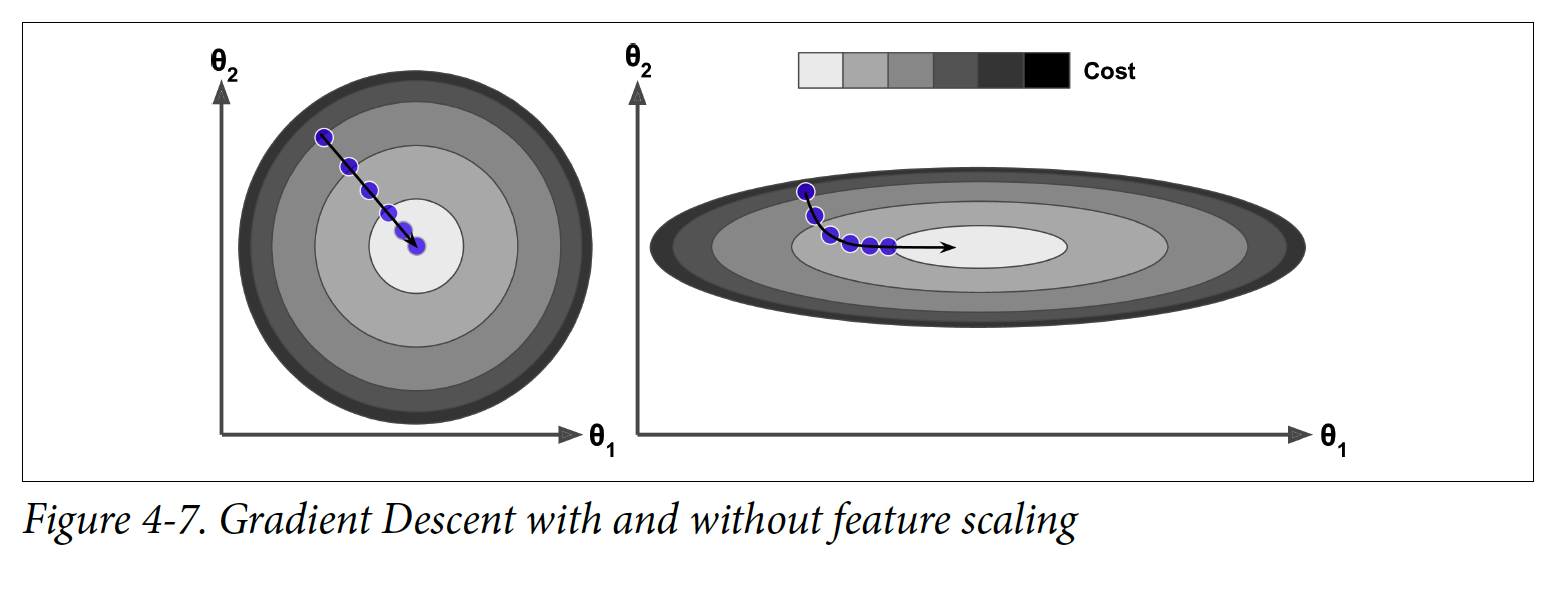
Linear regression 모델의 MSE cost function은 볼록 함수(convex function)이고, 이는 local minima는 없고 오직 하나의 global minimum만 있다는 것을 의미한다. 또한, 연속 함수이기 때문에 갑작스럽게 변화하지 않는다. 이러한 이유들 때문에 경사 하강법(gradient descent)은 global minimum 근처로 수렴하는 것이 보장된다.

Cost 함수는 bowl의 모양을 가지고 있다. 특징들의 scale이 다르면, bowl이 매우 길어질 수 있다. 왼쪽 그림 같은 경우는 training set에 대해 특징 1과 특징 2과 같은 scale이고, 오른쪽 그림은 특징 1의 값들이 특징 2보다 작기 때문에 길게 늘어졌다.

왼쪽 그림 경우에 경사 하강법(gradient descent)가 최소점에 직선으로 다가서지만, 오른쪽 그림의 경우에는 수렴하기까지 오래 걸리게 된다.

4.2.1 Batch Gradient Descent

Cost 함수의 경사(Gradient Descent)를 partial derivative(편미분)으로 찾아낸다. 밑에 식은 cost 함수가 MSE고 해당 함수에 편미분을 적용했다.

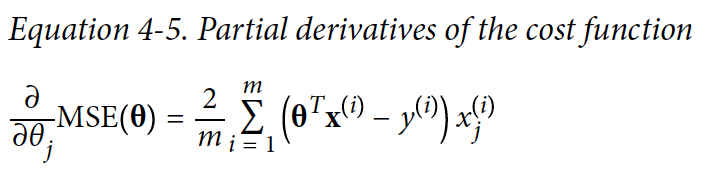
각각 인스턴스들에 편미분을 계산하는 대신에, 전체 cost 함수를 편미분 하는 방법은 다음과 같다:

Gradient vector가 구해지고 예를 들어 위 방향을 가리키면 밑 방향으로 이동을 하면 된다. 얼만큼 이동하는지는 learning rate의 값이 결정한다.

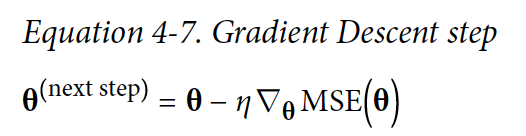
eta = 0.1 # learning rate
n_iterations = 1000
m = 100

theta = np.random.randn(2,1) # random initialization

for iteration in range(n_iterations):
    gradients = 2/m * X_b.T.dot(X_b.dot(theata) - y)
    theta = theata - eta * gradients

print(theta)
# array([[4.215xx], [2.7701xx]])

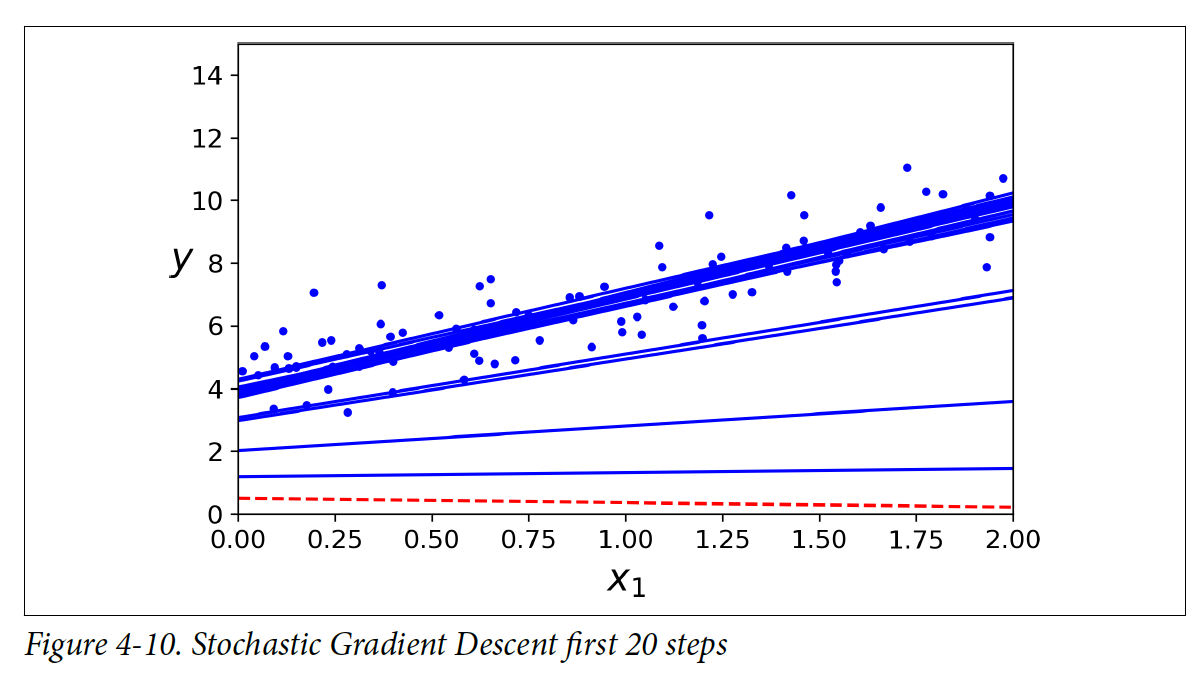
밑에 그림은 learning rate를 다르게 했을 때 첫 10 step동안 gradient descent가 어떻게 변화했는지 보여준다.

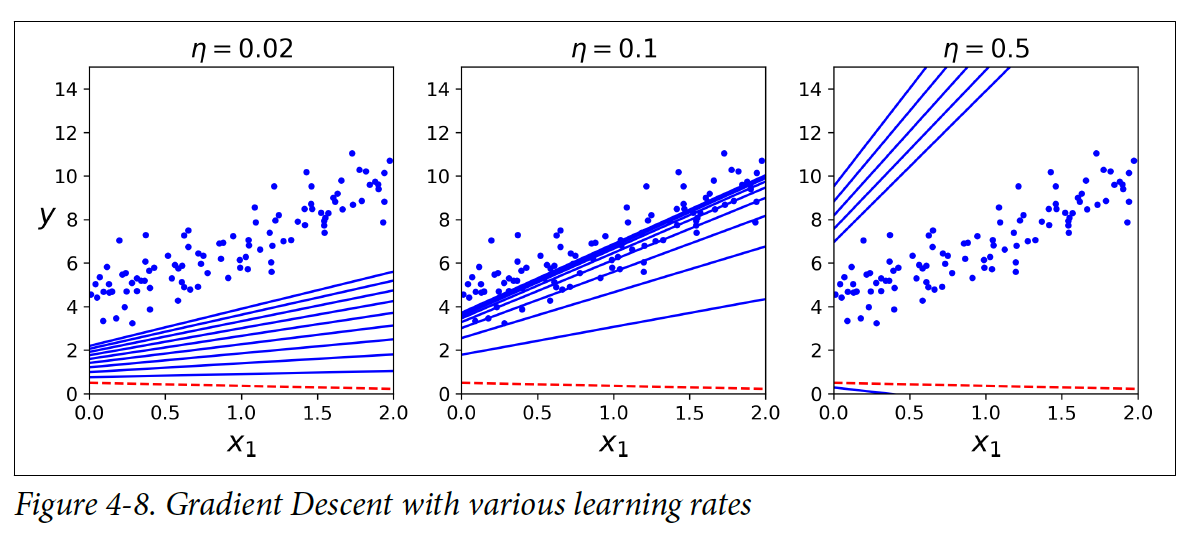
왼쪽 그림은 learning rate가 너무 낮기 때문에 수렴하기 까지 오래 거릴 것으로 보인다. 가운데 그림은 learning rate가 적절하게 설정이 되어서 제대로 수렴한 것처럼 보인다. 오른쪽 그림은 learning rate가 너무 높아서 값이 여기저기로 튀는 것을 볼 수 있다.

Learning rate를 적절한 값으로 설정하고 나서, iteration을 설정하는 가장 좋은 방법은 iteration의 수를 엄청 크게 설정을 한 다음에 gradient vector가 작아지면 알고리즘을 멈추는 것이다.

4.2.2 Stochastic Gradient Descent

Batch Gradient Descent의 단점은 gradient를 계산할 때 각 step에서 전체 training set을 사용하기 때문에 매우 느리다는 것이다. Stochastic Gradient Descent는 각 step에서 전체 trainig set중에서 랜덤하게 몇 개의 set만 선택 한 다음에 그 set들로만 gradient를 계산한다.

전체 training set을 한 step에서 학습하지 않기 때문에 cost 함수가 직선으로 수렴하지 않고 여기저기 튀다가 서서히 수렴하게 된다. 여기저기 튄다고 해서 꼭 나쁜 것 만은 아니다. 불규칙하게 이동을 하기 때문에 지역 minimum을 벗어나서 global minimum을 Batch Gradient Descent보다 더 잘 찾을 수도 있다. 하지만, 계속 튀기 때문에 알고리즘이 학습을 멈췄을 때 최종 파라미터의 값이 최적은 아닐 수 있다.

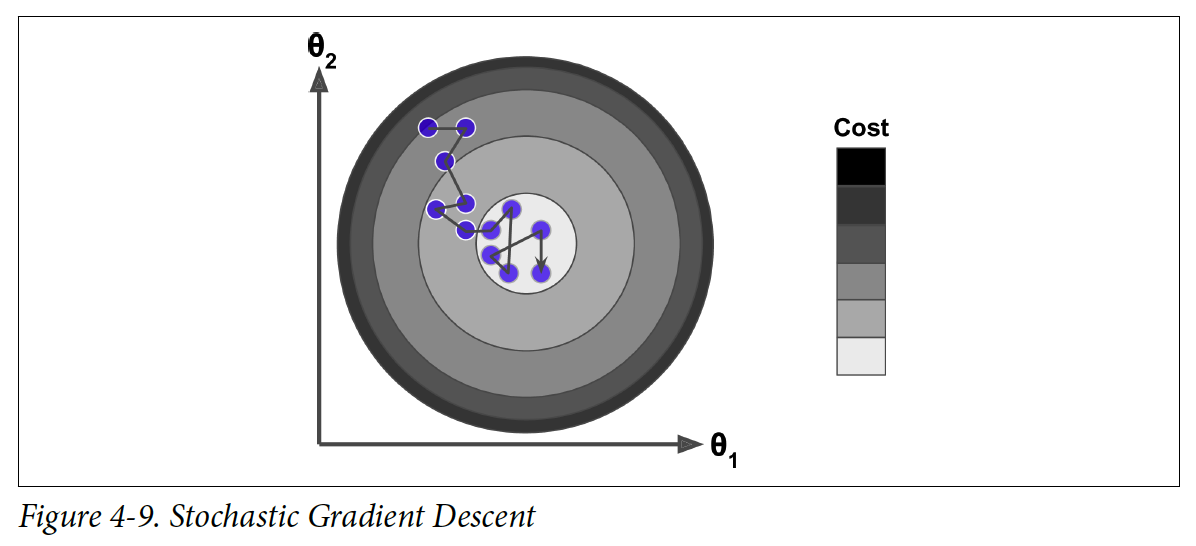
Global minimum에 도달하지 못하는 문제에 대한 해결책으로는 점진적으로 learning rate를 감소시키는 방법이 있다. 처음에는 learning rate를 크게 설정을 하고 점점 값을 줄여나가는 것이다. 각 iteration마다 learning rate를 결정하는 함수를 learning schedule이라고 부른다. Learning rate가 너무 빠르게 감소되면 local minimum에 멈출 가능성이 있고, 너무 느리면 mimimum에 너무 오래 남아 있을 가능성이 있다.

간단한 learning schedule을 사용한 Stochastic Gradient Descent의 코드이다:

n_epochs = 50
t0, t1 = 5, 50 #learning schedule hyperparameters
m = 100

def learning_schedule(t):
    return t0 / (t + t1)

theta = np.random.randn(2,1) # random initialization

for epoch in range(n_epochs):
    for i in range(m):
        random_index = np.random.randint(m)
        xi = X_b[random_index:random_index+1]
        yi = y[random_index:random_index+1]
        gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
        eta = learning_schedule(epoch * m + i)
        theta = theta - eta * gradients

print(theta)
# array([[4.2107xxx], [2.748xxx]])

각 iteration을 epoch이라고 부른다.

Linear Regression이 SGD를 사용하게 하려면 Scikit-Learn의 SGDRegressor 사용하면 된다. 이 클래스는 squared error cost 함수를 사용해서 최적화한다. 밑에 코드는 최대 1000 epochs를 실행하고 loss가 1e-3보다 낮아지면 멈춘다. Learning rate는 0.1부터 시작을 한다.

이 해결책도 Normal Equation으로 얻은 결과와 비슷하게 나온다.

from sklrean.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter = 1000, tol=1e-3, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel())

sgd_reg.intercept_, sgd_reg.coef_
# (array([4.24365]), array([2.8250xxx]) 

4.2.3 Mini-batch Gradient Descent

Mini-batch GD는 작은 instance들의 랜덤 set으로 gradient를 계산한다. Mini-batch GD는 GPU를 사용해서 성능을 끌어올릴 수 있다. Mini-batch GD는 SGD보다 minimum에 더 가까워질 수 있지만, local minima에서 벗어나기 더 힘들 수도 있다.

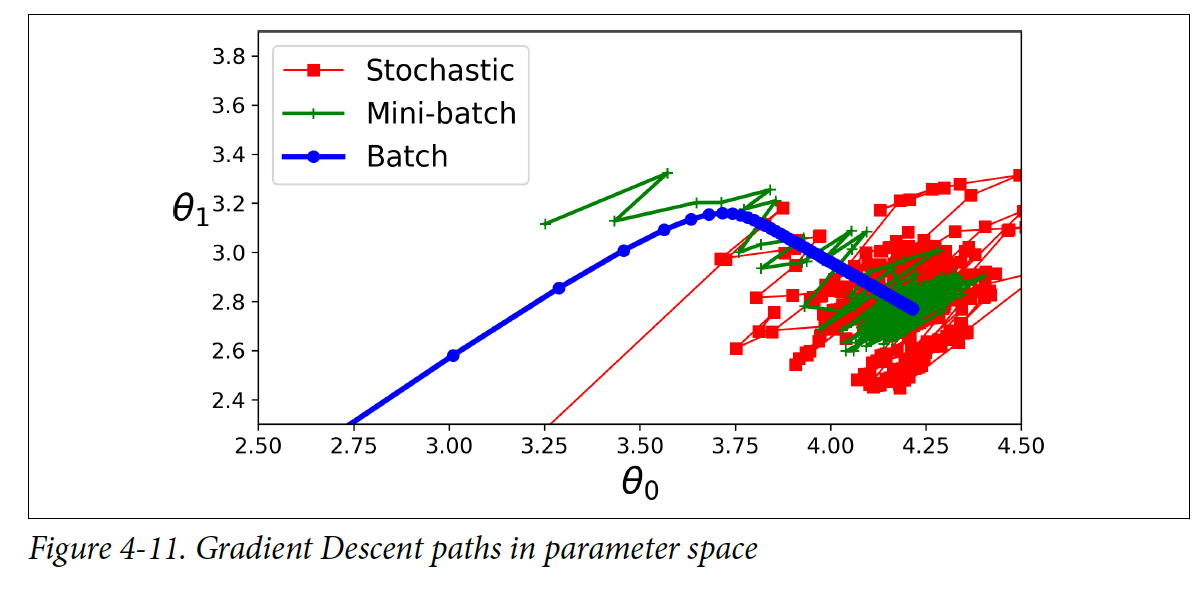
밑에 그림은 3가지의 경사 하강법(gradient descent) 알고리즘들이 학습하면서 어떻게 변화하는지 보여준다. Batch GD 같은 경우는 바로 최소점에 도달하지만, 나머지 두 알고리즘들은 최소점 근처에서도 계속 움직인다.

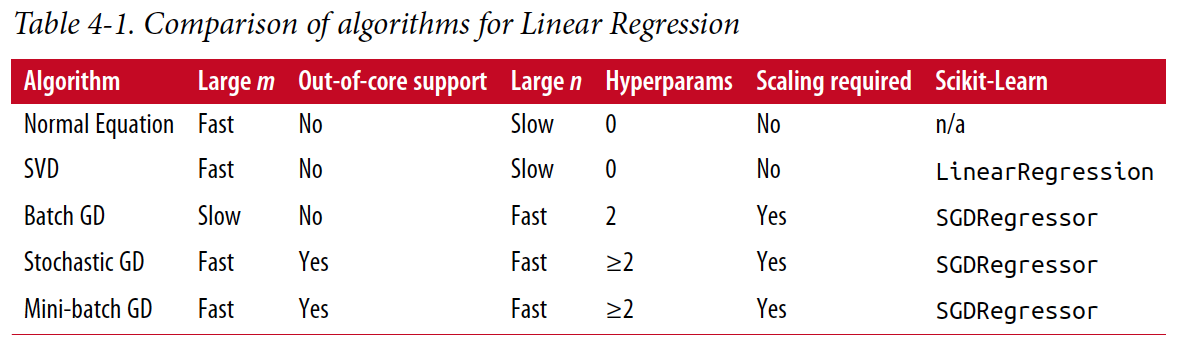
지금까지 배운 Linear Regresssion 알고리즘들을 정리하면 다음과 같다.

4.3 Polynomial Regression

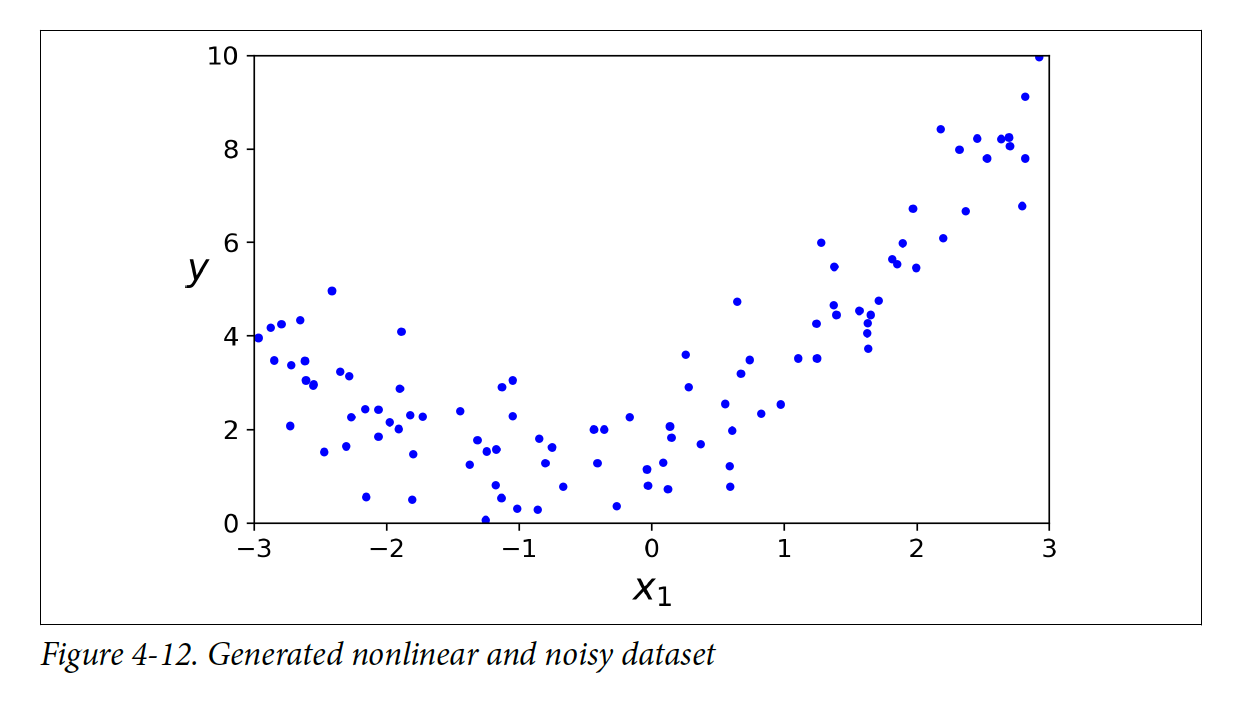
데이터가 위 예제들처럼 직선으로 표현이 안 되는 경우가 많다. 하지만, 이러한 경우에도 linear 모델을 사용할 수 있다, 이러한 방법을 Polynomical Regression이라고 부른다.

직선으로 표현이 불가능한 데이터를 만들어보려고 한다.

m = 100
X = 6 * np.random.rand(m,1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m,1)

위와 같은 데이터에는 PolynomicalFeatures 클래스를 사용해서 training 데이터를 변형하고, 각 특징(feature)들에 제곱을 해서 새로운 특징(feature)처럼 다룬다. (제곱을 하는 이유는, 데이터가 2차 방정식으로 구성되어있기 때문이다)

from sklrean.preprocessing import PolynomialFeatures

poly_features = PolynomicalFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0]
# array([-0.75275xxx])

X_poly[0]
# array([-0.75275xxx, 0.56664xxx])

X_poly는 기존의 특징(feature)들과 제곱된 특징(feature)를 포함하고 있다. 이제 이 데이터에 LinearRegression 모델을 사용할 수 있다.

lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
# array([1.7813xxx]), array([[0.93366xxx], [0.56456xxx]])

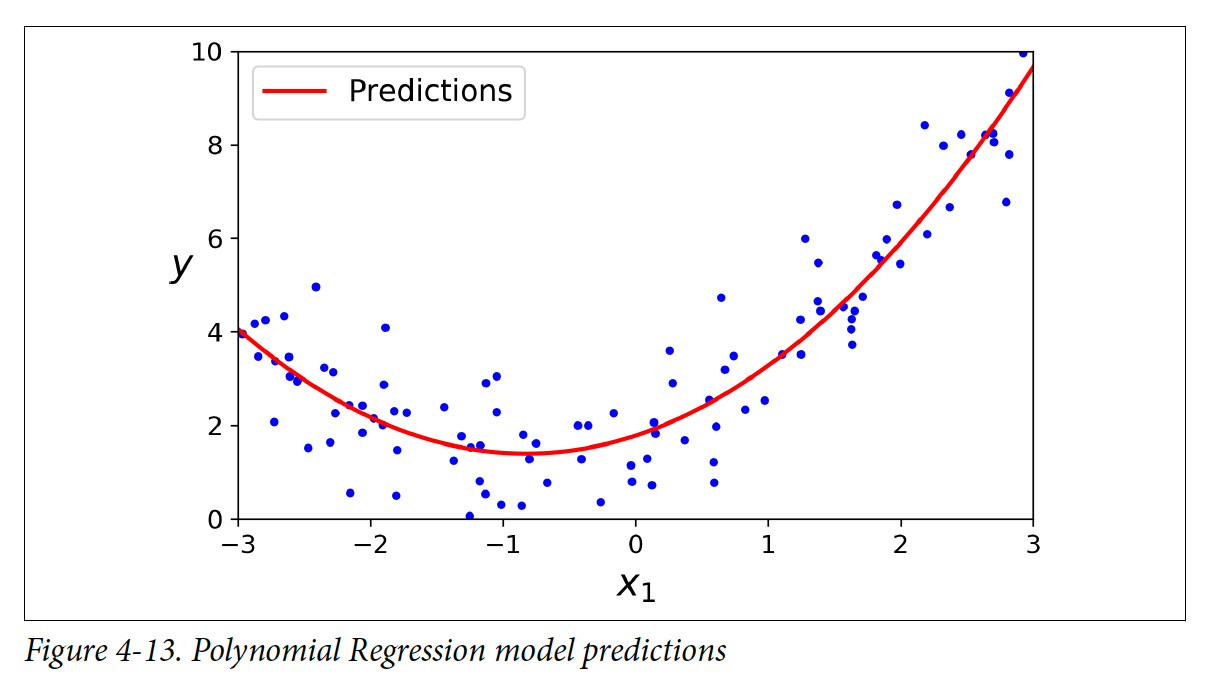
특징(feature)들이 여러개 있을 때, Polynomical Regression은 특징(feature)들간 관계를 찾아낼 수 있다. 주어진 degree내에 모든 조합들을 생성해낸다. 예를 들어, degree=3이면, a^2, a^3, b^2, b^3 뿐만 아니라 ab, a^2b, ab^2의 조합도 찾아내는 것이다. 특징(feature)의 수가 많아질 수록 이 조합의 수도 매우 커지게 된다.

4.4 Learning Curves

Degree가 높아질 수록(=모델이 복잡해질 수록) Polynomial Regression은 training 데이터에 오버피팅(overfitting)하게 되고 낮을 수록 언더피팅(underfitting)하게 된다.

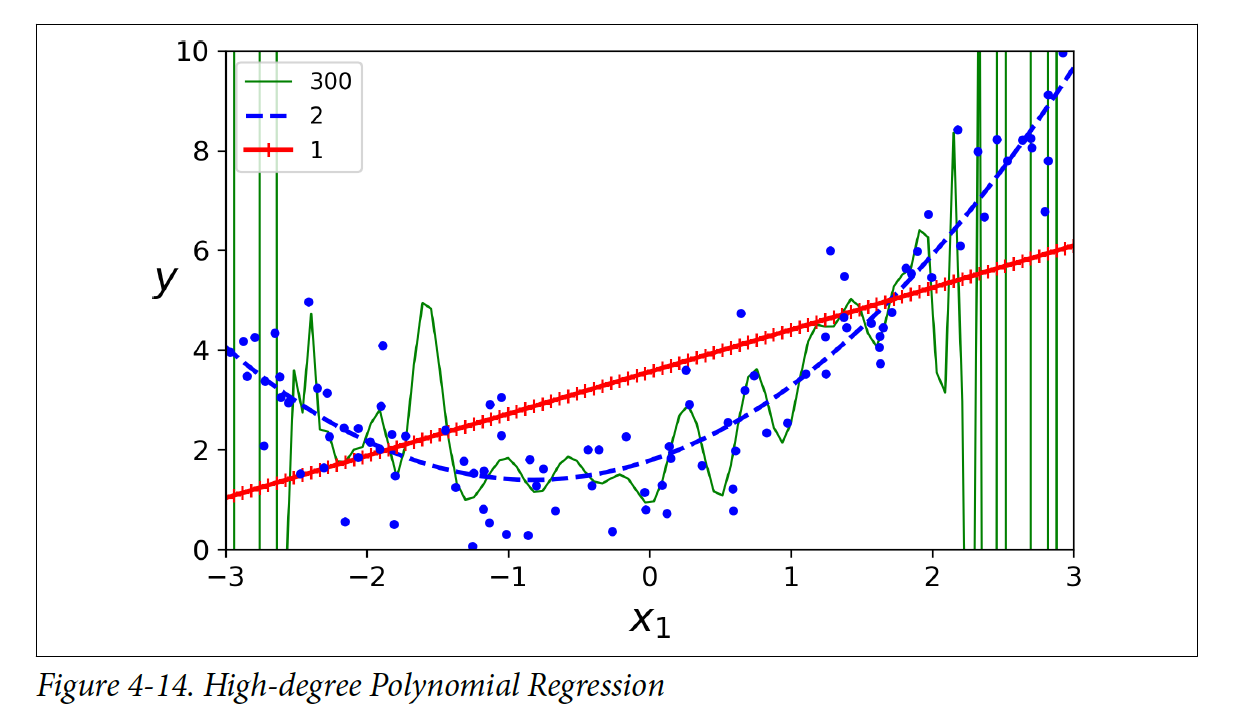
하지만, 문제를 해결하려고 할 때 모델이 얼마나 복잡해야 하는지 알기 힘들고, 모델이 데이터에 오버피팅(overfitting)하는지 언더피팅(underfitting)하는지 알기 힘들다. 이러한 경우에는 learnig curve를 보면 모델이 오버피팅(overfitting)하는지 언더피팅(underfitting) 알 수 있게 된다.

밑에는 training 데이터에 대한 모델의 learnig curve를 그래프로 그려주는 코드이다.

from skleran.metrics import mean_squared_error
from sklrean.model_selection import train_test_split

def plot_learning_curves(model, X, y):
    X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)
    train_errors, val_errors = [], []
    for m in range(1, len(X_train)):
        model.fit(X_train[:m], y_train[:m])
        y_train_predict = model.predict(X_train[:m])
        y_val_predict = model.predict(X_val)
        train.errors.append(mean_squared_error(y_train[:m], y_train_predict))
        val_errors.append(mean_squared_error(y_val, y_val_predict))
    
    plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")
    plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")

lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)

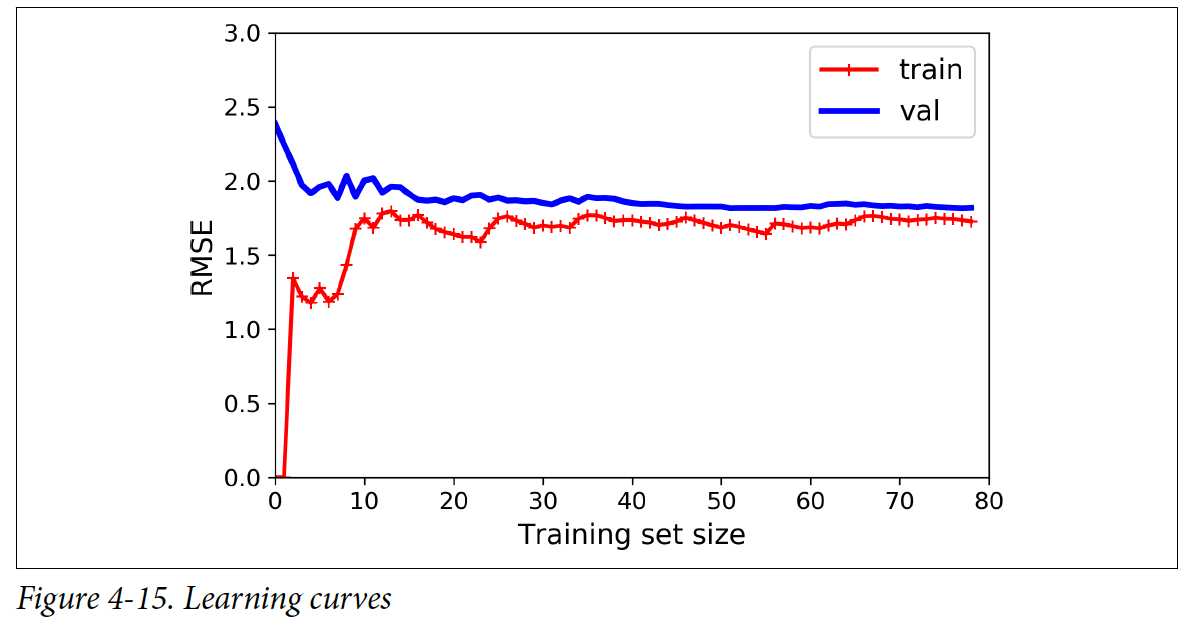
Training 데이터 set의 크기에 따른 모델의 성능을 나타내는 그래프이다. Training set이 한개 혹은 두개 일 때는 모델이 완벽하게 fit하기 때문에 RMSE값이 0에 가깝다. 하지만, training set의 크기가 커질 수록 모델이 데이터에 fit하기 어려워진다. RMSE 값이 커지다가 어느 시점에 도달하면 training set이 더 커져도 평균 에러가 크게 변하지 않는다.

이제 validation 데이터를 보면 처음에 training set이 적을 때 에러율이 가장 높은 것을 볼 수 있다. 이는 모델이 적은 수에만 학습이 되어서 전체 데이터를 일반화를 아직 못하기 때문에 발생한다. Training set의 크기가 커질 수록 validation 에러도 점점 줄어들다가 어느 시점에 도달하면 에러율이 일정해진다.

10-degree polynomial 모델에도 같은 데이터를 적용해서 비교를 해보자

from sklearn.pipeline import Pipeline

polynomial_regression = Pipeline([
            ("poly_features", PolynomicalFeatures(degree=20, include_bias=False)),
            ("lin_reg", LinearRegression()),
        ])

plot_learning_curves(polynomial_regression, X, y)

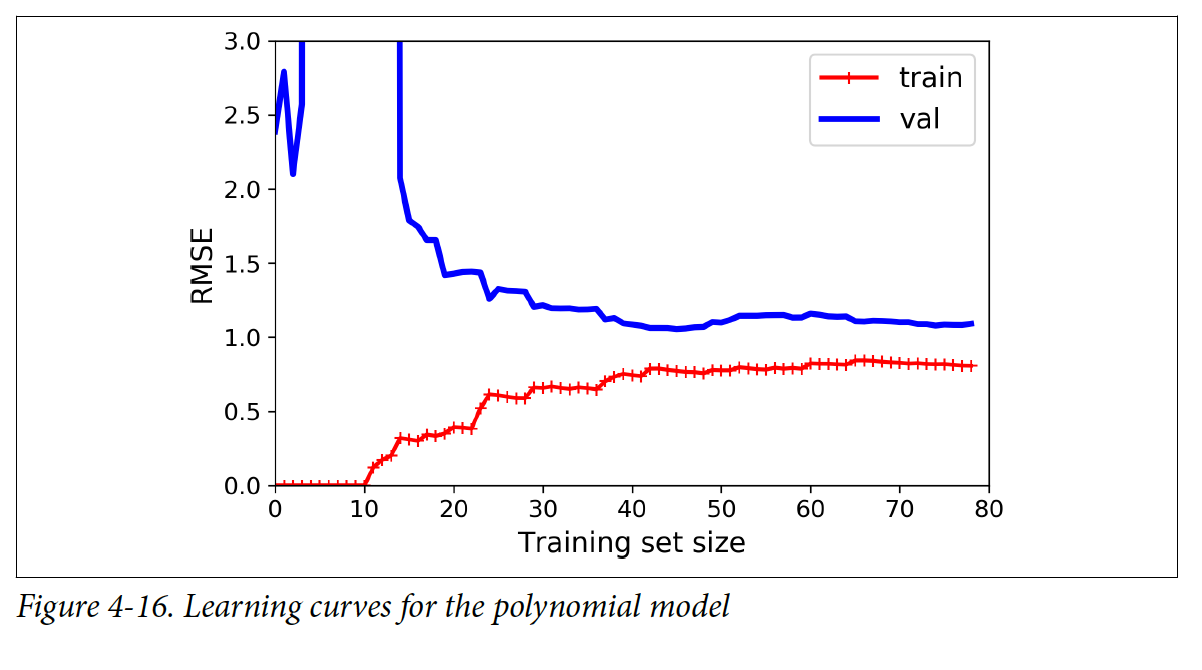
Linear Regression모델과 그래프가 비슷해보이지만 2가지가 다르다:

LinearRegression 모델보다 training 데이터에 에러가 더 낮다
Curve간 차이가 Linear Regression모델보다 크다. 모델이 training 데이터에 더 잘 fit한다는 의미이다(overfitting 발생했다는 의미이기도 하다). 하지만 training set의 크기가 커질 수록 두 curve들이 가까워진다.

4.4.1 The Bias/Variance Tradeoff

머신러닝에서 모델의 일반화 오차(generalization error)는 3가지의 다른 오차들의 합으로 나타낼 수 있다.

편향(Bias)

잘못된 가정 때문에 생기는 일반화 오차이다. 예를 들어, 4차원식의 데이터인데 1차원이라고 가정을 하는 것이다. 이러한 경우에는 주로 training 데이터에 언더피팅(underfitting)하게 된다.
분산(Variance)

Training 데이터의 작은 변화(variation)에 너무 민감해서 생기는 일반화 오차이다. Degree가 높으면 높은 분산을 갖게 되고 그러면 training 데이터에 오버피팅(overfitting)하게 된다.
줄일 수 없는 오차(Irreducible Error)

데이터 자체의 노이즈 때문에 발생하는 오차이다. 이 오차를 줄이기 위해서는 데이터를 잘 정리 및 처리해야 한다.

여기서 tradeoff가 발생한다

→ 모델의 복잡도를 늘리면 분산(variance)가 늘어나고 편향(bias)가 줄어든다. 반면에 복잡도를 줄이면 편향(bias)가 늘어나고 분산(variance)가 줄어든다.

4.5 Regularized Linear Models

오버피팅(overfitting)을 피하기 위해서 모델을 정규화(regularize)해야 한다. 예를 들어, polynomial 모델을 정규화하려면 degree의 값을 줄이면 된다.

Linear 모델 같은 경우에는 가중치(weights)를 제한해서 정규화를 한다. 가중치(weights)를 제한하는 방법으로는 3가지가 있다: Ridge Regression, Lasso Regression, Elastic Net

4.5.1 Ridge Regression

Ridge Regression은 Linear Regression의 정규화된 버전이다.

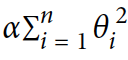
라는 regularization term이 cost 함수에 더해진다. 이 식은 학습하는 알고리즘이 데이터에 fit하게 해주고 가중치(weights)를 가능한 작게 유지한다.

**주의: Regularization term은 학습할 때 cost 함수에만 더해져야한다.

α라는 하이퍼파라미터로 모델을 얼마나 정규화할지 조절을 할 수 있다. α=0이면 Ridge Regression은 그냥 Linear Regression이다. α가 크면, 모든 가중치(weight)들이 0에 가까워지고 결과는 데이터의 평균을 지나가는 평평한 선이 된다.

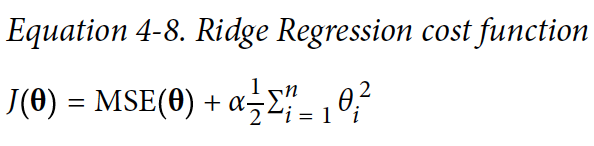
** Ridge regression을 적용하기 전에 데이터를 scale하는 것이 중요하다(e.g. StandardScaler를 사용)

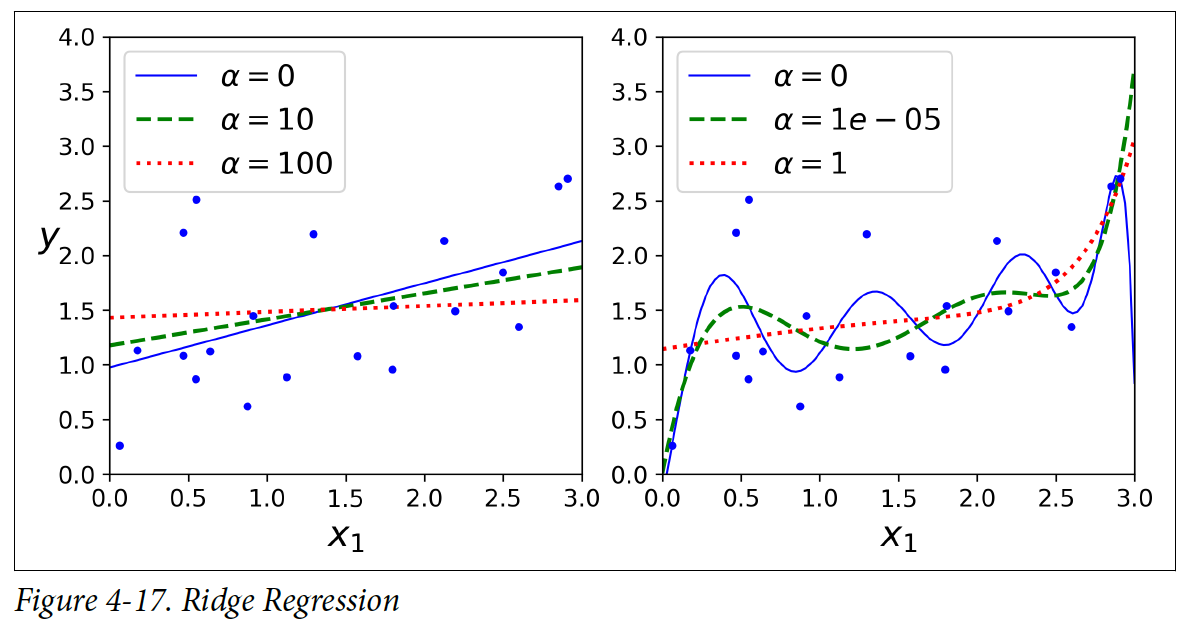
왼쪽 그림은 linear한 모델이 사용되었고, 오른쪽 그림에는 PolynomicalFeature(degree=10)으로 확장한 다음에 StandardScaler로 scale을 했다. α의 값이 클수록 모델이 더 평평해지는 것을 볼 수 있다. 분산(variance)은 줄어들지만, 편향(bias)은 높아진다.

Scikit-Learn으로 Ridge Regression을 밑의 코드로 실행할 수 있다. closed-from equation으로 Ridge Regression을 실행할 수 있고, Gradient Descent를 사용해서도 실행할 수 있다.

from sklearn.linear_model import Ridge
# closed-form equation 사용
ridge_reg = Ridge(alpha=1, solver="cholesky")
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
# array([[1.550xx]])

# gradient descent 사용
sgd_reg = SGDRegressor(penalty="l2")
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])
# array([1.47012xxx])

4.5.2 Lasso Regression

Lasso Regression은 Linear Regression의 다른 정규화된 버전이다. Ridge Regression처럼 regularization term을 cost 함수에 더해주지만, 가중치(weight) 벡터의 l1 norm을 사용한다.

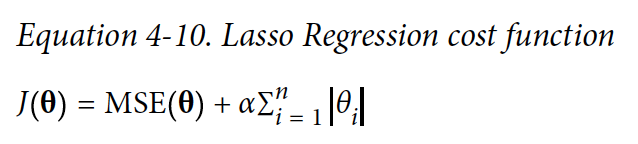
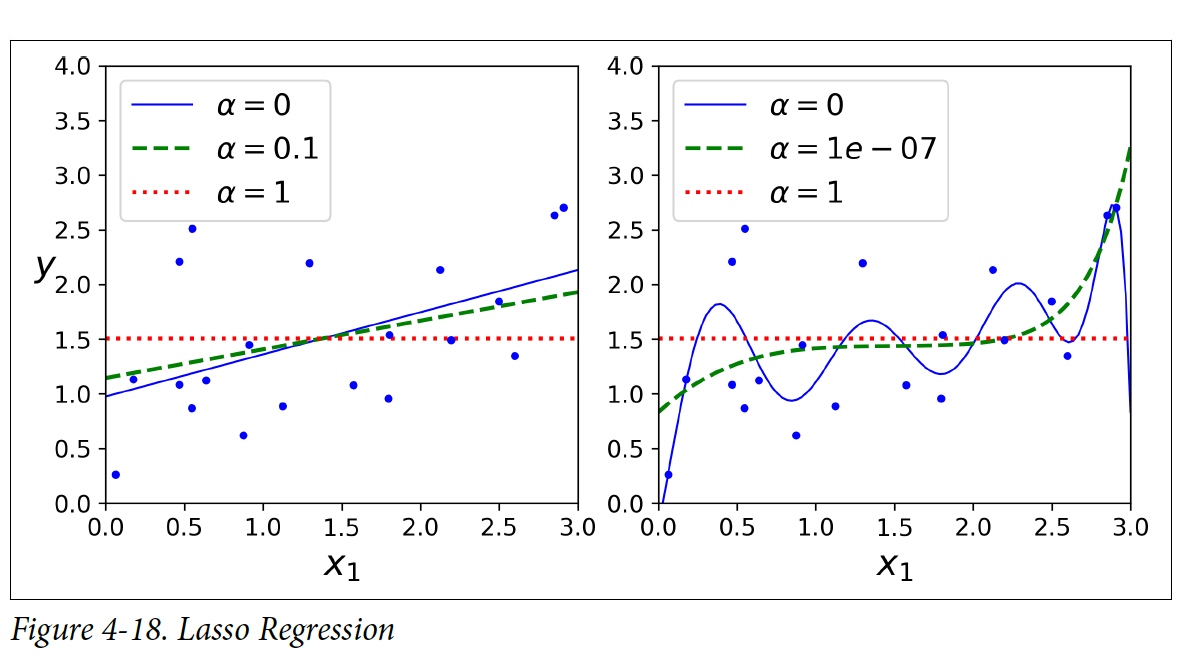
Lasso Regression의 특이점으로는 중요하지 않은 특징(feature)들의 가중치(weight)들을 완전하게 제거하는 경향이 있다는 것이다.

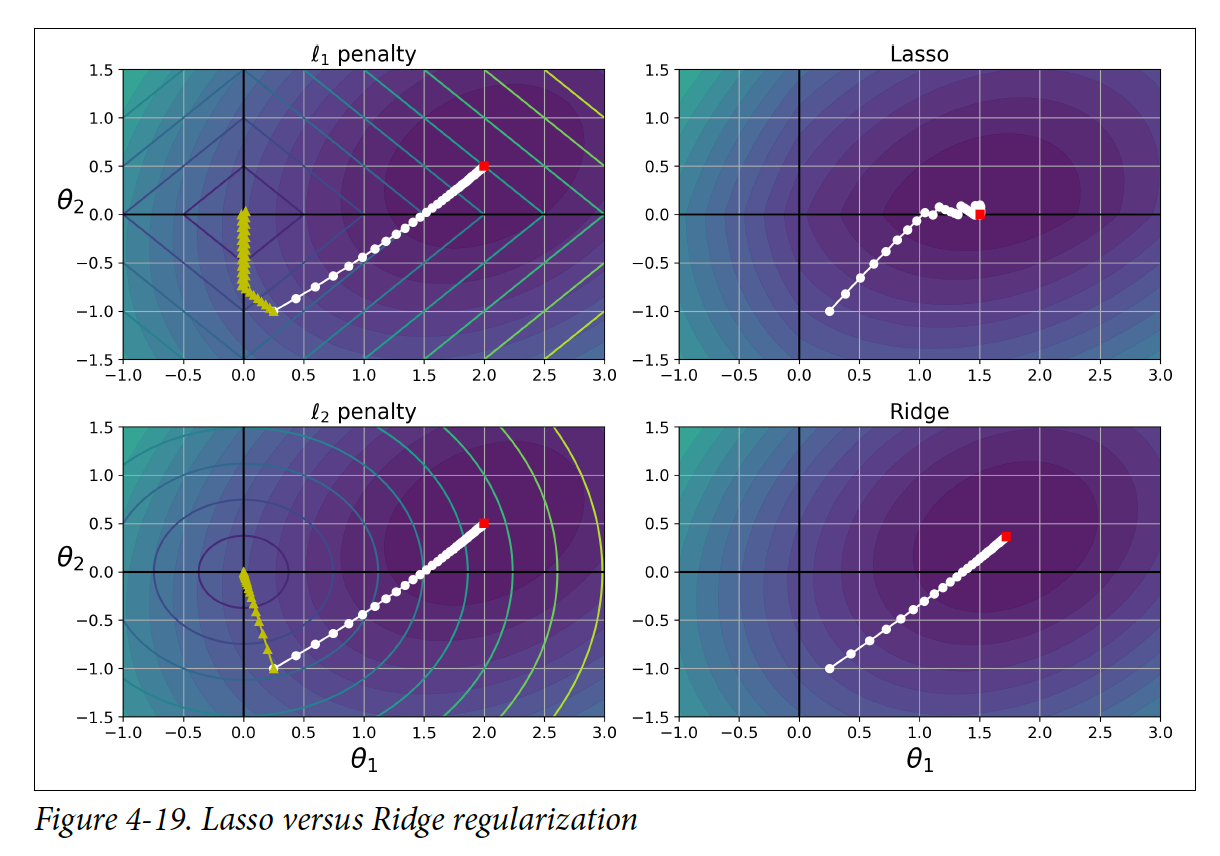
θ _2 = 0이 global minimum이다. 왼쪽 두 그림은 정규화되지 않은 cost함수들이고, 오른쪽 두 그림은 정규화된 Lasso와 Ridge를 나타낸다. 위 두 그림은 l1 penalty를 사용하고 밑 두 그림은 l2 penalty를 사용한다. 그림을 보면 알 수 있듯이, 정규화된 minimum이 정규화되지 않은 minimum보다 θ = 0 더 가깝다.

Lasso cost 함수는 θi=0에서 미분 불가능하다. 하지만, Subgradient vector를 사용하면 θ=0일 때도 경사 하강(gradient descent)가 잘 작동한다.

밑에는 Lasso 클래스를 사용한 간단한 예제이다. 단순하게 SGDRegressor(penalty="l1")로도 같은 결과를 만들어낼 수 있다.

from sklearn.linear_model import Lasso

lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X,y)
lasso_reg.predict([[1.5]])
# array([1.53788174])

4.5.3 Elastic Net

Elastic Net은 Ridge Regression과 Lasso Regression 중간쯤에 있다. Regularization term은 두 개의 term을 합친것과 같고 mix ratio r을 조절할 수 있다. r=0이면, Elastic Net은 Ridge Regression과 동일하고 r=1이면 Lasso Regression과 동일하다.

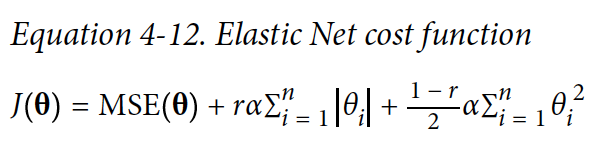
그렇다면 언제 Ridge, Lasso, Elastic Net 사용해야 하는가? Plain한 Linear Regression만 사용해도 괜찮은가?

일반적으로 plain한 Linear Regression을 사용하기 보다, 정규화를 조금이라도 적용하는 것이 좋다. Default로 Ridge를 사용하는 것도 좋지만, 몇개의 특징(feature)들만 유용하다고 생각될 때는 Lasso나 Elastic Net 사용하는 것이 낫다.

보통 Elastic Net이 Lasso보다 선호되는데 그 이유는 특징(feature)들의 수가 training instance보다 큰 경우나, 특징(feature)들이 서로 강한 상관관계를 지닌 경우에 Lasso가 제대로 작동을 하지 않는다.

from sklear.linear_model import ElasticNet

elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X,y)
elastic_net.predict([[1.5]])
# array([1.54333xxx])

4.5.4 Early Stopping

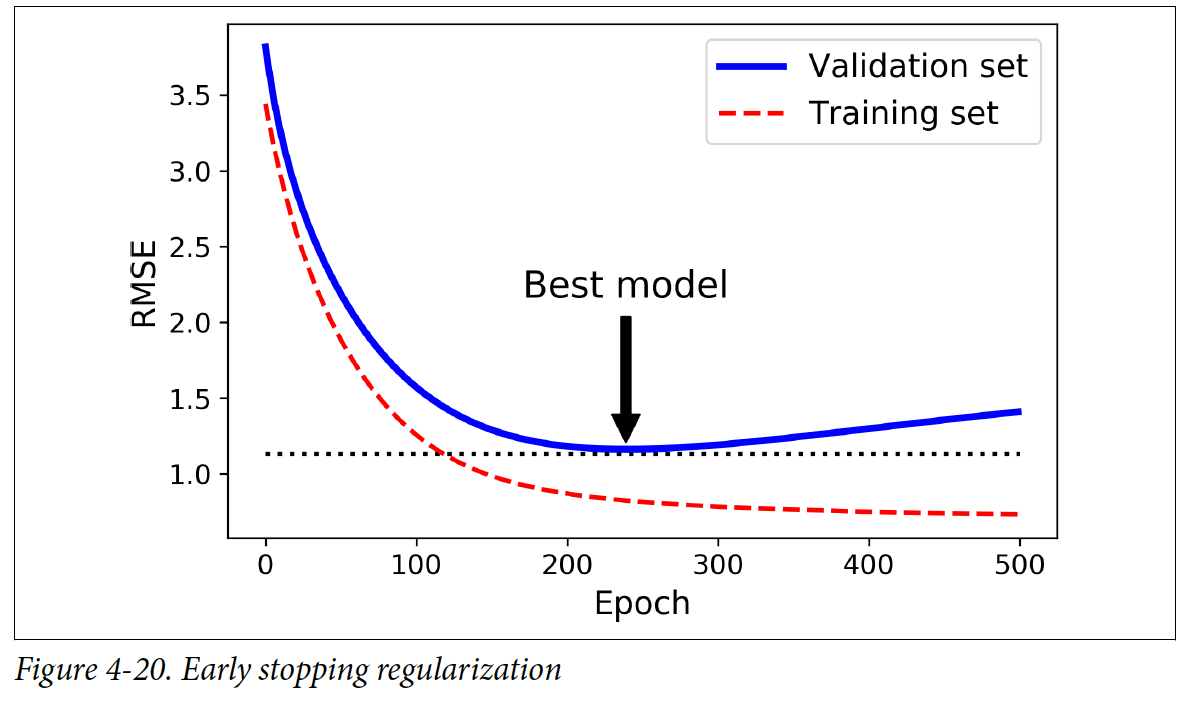
Early Stopping도 정규화하는 방법 중 하나이고, validation error가 minimum에 도달할 때 학습을 종료하는 것이다.

Epoch이 지남에 따라 알고리즘이 학습을 하고 training set이나 validation set의 prediction error(RMSE)도 점점 줄어든다. 하지만, 어느 시점을 넘어서면 validation error가 다시 증가하게 된다. 보통 이 시점은 모델이 training 데이터에 오버피팅(overfitting)하게 되는 시점이다. 이러한 상황에 도달하면 학습을 종료하는 것이 좋은 방법이다.

from sklearn.base import clone

# prepare the data
poly_scaler = Pipeline([
    ("poly_features", PolynomicalFeatures(degree=90, include_bias=False)),
    ("std_scaler", StandardScaler()))	
])

X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)

sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True, penalty=None, learning_rate="constant", eta0=0.0005)

minimum_val_error = float("inf")
best_epoch=None
best_model=None
for epoch in range(1000):
    sgd_reg.fit(X_train_poly_scaled, y_train) # Continues where it left off
    y_val_predict=sgd_reg.predict(X_val_poly_scaled)
    val_error = mean_squared_error(y_val, y_val_predict)
    if val_error < minimum_val_error:
        minimum_val_error = val_error
        best_epoch = epoch
        best_model = clone(sgd_reg)

4.6 Logistic Regression

Logistic Regression은 instance가 특정한 class에 속할 확률을 측정하는데 사용된다.

4.6.1 Estimating Probabilities

Linear Regression처럼 Logistic Regression 모델도 입력 특징(feature) + 편향(bias term)들의 가중치 합(weighted sum)을 계산한다. 그 다음에는 Linear Regression처럼 결과를 바로 보여주는 대신에, logistic한 결과를 보여준다.

작은 theata는 sigmoid 함수이고 0과 1중 하나를 결과로 낸다.

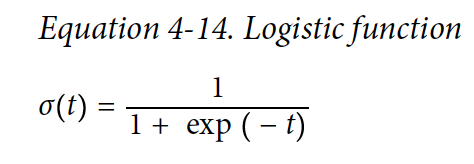
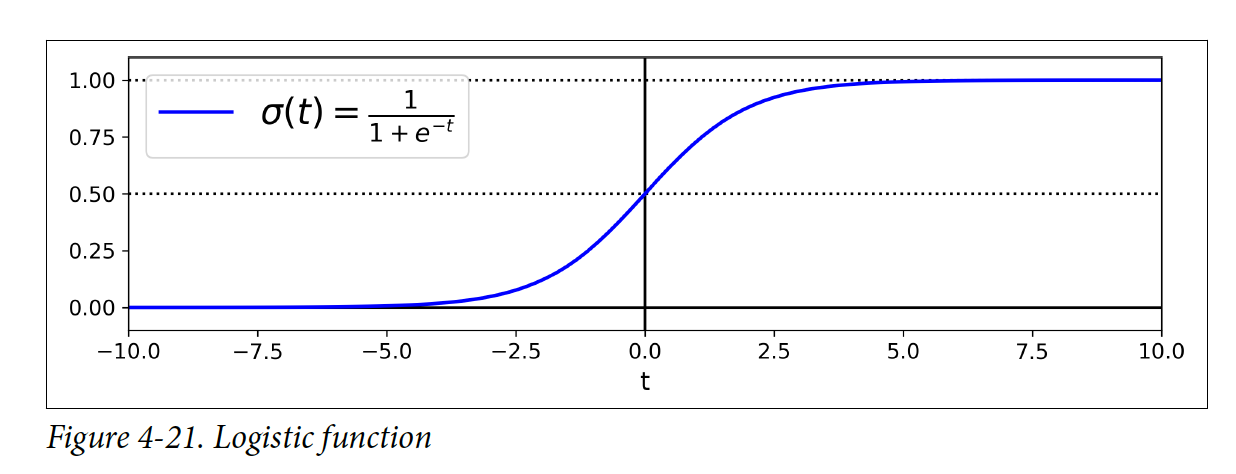
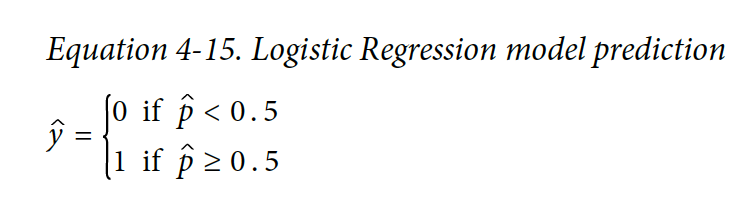
t < 0 일 때 sigmoid 함수 < 0.5 가 되고 Logistic Regression 모델은 0으로 예측하고, t ≥ 0 이고 sigmoid 함수 ≥ 0.5 일 떄 1로 예측한다.

4.6.2 Training and Cost Function

Logistic Regression을 학습할 때 모델이 (y=1)인 instance들에 높은 확률을 측정하고 (y=0)인 instance들에 낮은 확률을 측정하도록 θ 파라미터 벡터를 설정해야 한다.

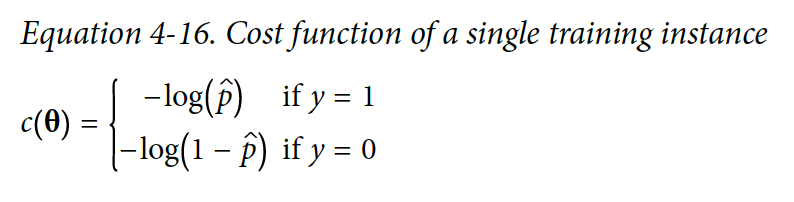
t가 0에 가까워질 수록 -log(t)는 매우 커진다. 그렇기 때문에 1로 예측해야 하는 instance를 0으로 예측을 했을 때 cost함수의 값이 매우 커지게 될 것이다. 0으로 예측해야 하는 instance를 1로 예측했을 때도 비슷하게 작동한다반면에, -log(t)는 t가 1에 가까워질수록 0에 가까워진다. 즉, 제대로 분류가 되었을 때는 cost가 0에 가까워지게 되는 것이다.

전체 training set에 대한 cost 함수는 각각 instance들의 cost를 평균을 한 것이다. 그렇기에 cost 함수를 log loss로 나타낼 수 있다.

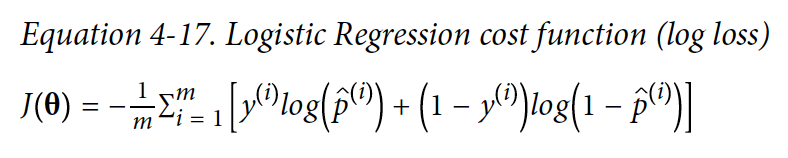
Logistic Regression에는 Normal Equation과 같은 closed-form equation이 없다. 하지만 cost함수가 Linear Regression처럼 볼록(convex)하기 때문에 경사 하강법(Gradient Descent)으로 global minimum을 찾는 것이 보장된다.

Cost 함수의 편미분분은 다음과 같다:

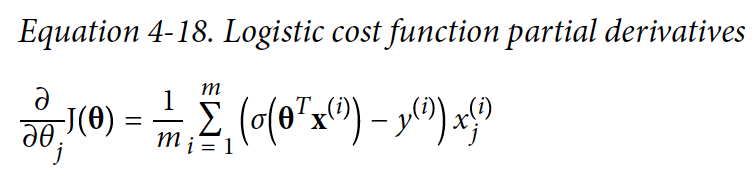
편미분하는 식이 Linear Regression에서 BGD의 cost 함수의 편미분을 구할 때와 유사하다.

4.6.3 Decision Boundaries

Decision Boundary에 대해 알아보기 위해 iris 데이터를 사용해보려고 한다. 이 데이터셋은 3가지 종류의 iris 꽃의 꽃받침(sepal)과 꽃잎(petal)의 길이 및 너비에 대한 정보를 지니고 있다.

데이터 셋을 불러오고 나서 Logistic Regression 모델을 학습을 한 다음에 꽃잎(petal)의 너비가 0~3cm에 따라서 어떻게 예측되는지 보려고 한다.

from sklearn import datasets
from sklearn.linear_model import LogisticRegression

iris = datasets.load_iris()

X = iris['data'][:, 3:] # petal width
y = (iris['target']==2).astype(np.int)

log_reg = LogisticRegression()
log_reg.fit(X,y)

X_new = np.linspace(0,3,1000).reshape(-1,1)
_proba=log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:,1], "g-", label="Iris-Virginica")
plt.plot(X_new, y_proba[:,0], "b--", label="Not Iris-Virginica")

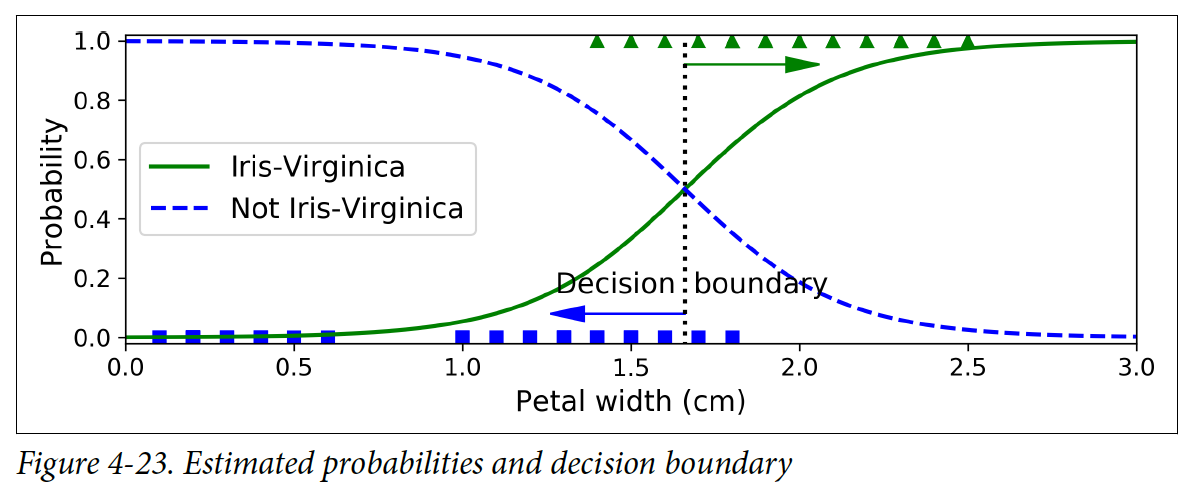
Iris-Virginica 라는 종류의 iris 꽃의 꽃잎(petal) 너비는 1.4 ~ 2.5 cm이다. 반면 다른 iris 꽃들의 꽃잎(petal)너비는 0.1 ~ 1.8cm이다. 그렇기 때문에 주어진 꽃의 꽃잎(petal)너비가 2cm가 넘으면 모델은 높은 확률로 Iris-Virginica라고 예측한다. 그리고 1 cm 이하이면 높은 확률로 다른 종류의 꽃이라고 예측을 한다.

1~2cm 사이에 있는 꽃들은 정확하게 예측이 되지 않는다. 이러한 꽃이 입력으로 들어오면 그나마 더 적합하다고 생각되는 class를 리턴하게 된다. 그렇기 때문에 약 1.6cm 근처에 decision boundary가 형성된다. 1.6cm 이상이면 Iris-Virginica로 분류하고, 이하면 다른 종류의 꽃으로 분류한다.

log_reg.predict([[1.7],[1.5]])
# array([1.0]) 

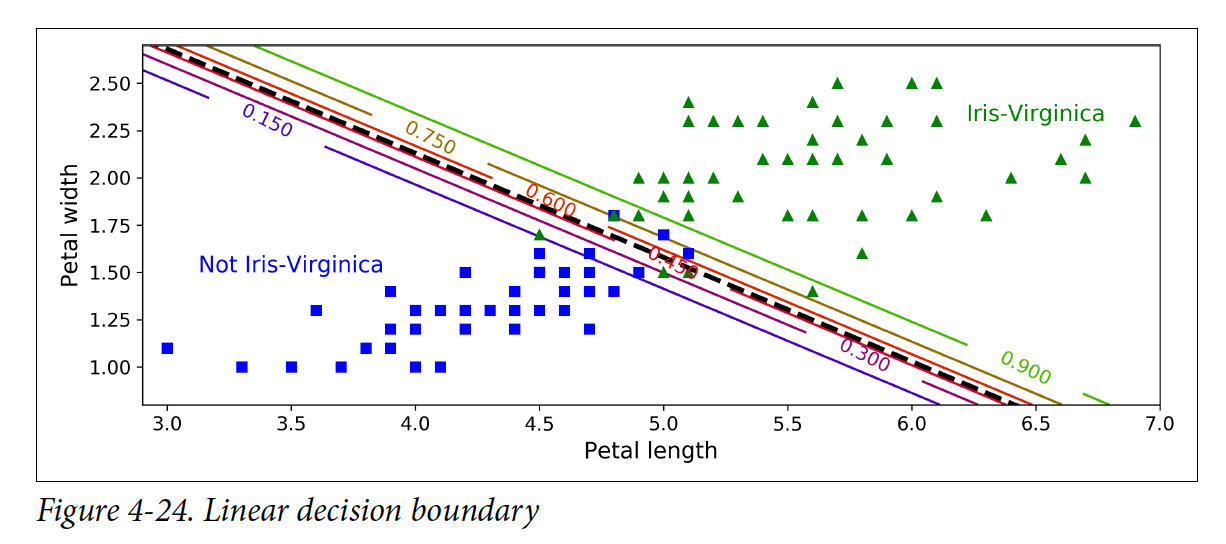
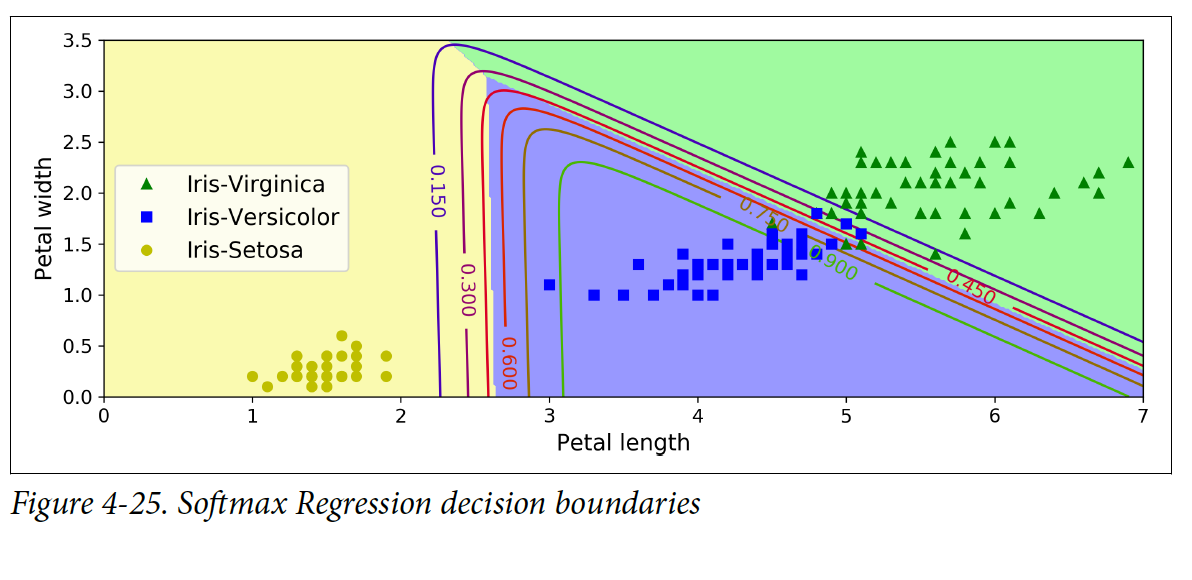
밑에 그림은 꽃잎(petal) 너비와 길이를 보여준다. 점선으로 되어 있는 선은 모델의 decision boundary를 나타낸다. 점선을 기준으로 오르쪽 위에 해당하는 꽃들은 Iris-Virginica로 분류된다.

다른 linear 모델들처럼 Logistic Regression 모델도 l1 or l2 penalty로 정규화할 수 있다. Scikit-Learn은 default로 l2 penalty를 더한다.

4.6.4 Softmax Regression

여러개의 binary 분류기(classifier)들을 학습하고 합칠 필요 없이 Softmax Regression을 사용하면 Logistic Regression 모델로 여러 class들을 바로 분류할 수 있다.

기본적인 아이디어는 다음과 같다: instance x가 주어졌을 때, Softmax Regression 모델이 각 class k에 대해 s_k(x) 점수를 계산한다.

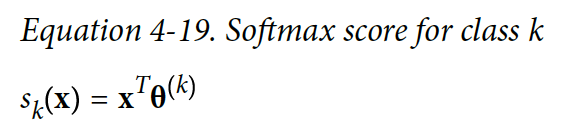
각 class에 대해 점수가 계산되면, softmax 함수에 점수들을 넣어서 class별로 확률을 측정할 수 있다. Softmax는 각 점수의 지수를 계산한 다음에 정규화를 한다.

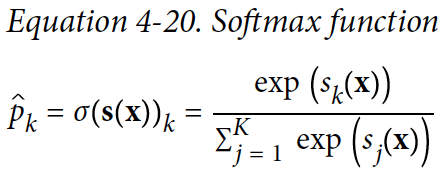
K는 class의 수이다
s(x)는 instance x에 대해 각 class의 점수를 포함하는 벡터이다.
theta(s(x))_k는 점수가 주어졌을 때 x가 class k로 특정된 확률을 의미한다

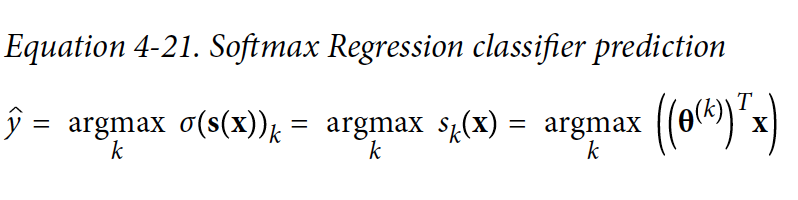
argmax 연산자는 함수를 최대화하는 값을 리턴한다. 할 수 있는 값을 리턴한다.

Cost 함수를 최소화하는 함수를 cross entropy라고 부른다.

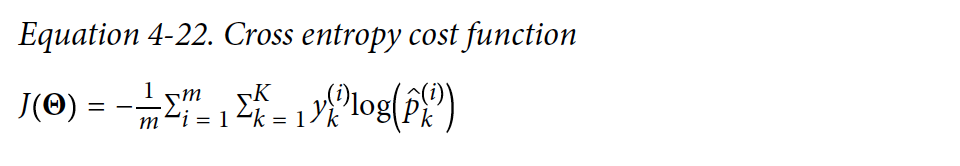
y_k는 i 번째 instance가 class k에 속하는 확률이다, 값은 1 혹은 0이다. 1 이면 instance가 해당 class에 속한다는 의미이다.

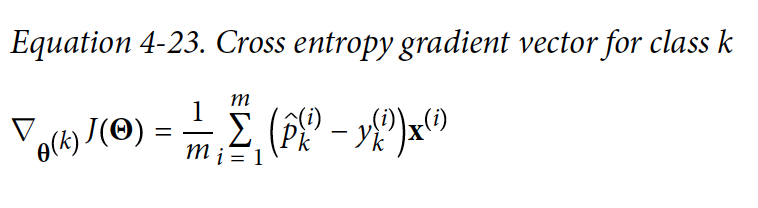
Scikit-Learn의 LogisticRegression은 기본적으로 OVA이지만, multi-class 파라미터를 “multinomial”로 변경하면 Softmax Regression을 사용할 수 있다. 이 때 solver도 반드시 명시해줘야 한다. Softmax Regression이 사용되면 l2 정규화가 default로 적용된다, C 라는 하이퍼파라미터로 값을 조절할 수 있다.

X = iris["data"][:,(2,3)]  # petal length, petal width
y = iris["target"]

softmax_reg = LogisticRegression(multi_class="multinomial", solver="lbfgs", C=10)
softmax_reg.fit(X,y)

softmax_reg.predict([[5,2]])
# array([2])

softmax_reg.predict_proba([[5,2]])
# array([[6.38xxe-07, 5.74xxe-02, 9.42xxe-01]])

[핸즈온 머신러닝-4] Training Models