Dynamic Programming(동적 계획법)

Dynamic Programming(동적 계획법)이란, 하나의 문제를 여러개의 작은 문제들로 나눠서 푸는 기법이다. 이 때 각각의 문제들은 sub-problem이라고 불리고, 항상 최적(optimal)한 해결책을 가지고 있어야 한다. Sub-problem의 최적화된 해결책을 가지고 더 큰 문제를 해결한다.

DP로 풀어서 속도를 확연하게 향상시킬 수 있는 문제가 바로 피보나치 수열 문제이다.

Fibo(N) = Fibo(n-1)+Fibo(n-2) (단, Fibo(0)=1, Fibo(1) = 1)

피보나치 수열을 처음 배울 때 보통 재귀(recursion)으로 푸는 방법을 배운다. 종료 조건인 Fibo가 0일 때와 1일 때를 설정해놓고, 그 이외의 숫자가 들어올 때는 재귀적으로 자기 함수를 다시 부르도록 구현을 한다. 재귀함수를 보면 모든 조건들이 깔끔하게 눈에 들어오기 때문에 구현하는 것이 상대적으로 쉽다.

def fibo(n):
    if n == 0:
        return 1
    if n == 1:
        return 1
    return fibo(n-1) + fibo(n-2)

하지만, 재귀로 피보나치 수열을 풀게 되면 밑의 그림과 같이 중복된 연산을 반복하게 된다. 예를 들어, Fibo(3)은 2번 계산되고, Fibo(2)는 3번 계산된다. 값은 항상 동일하기 떄문에 연산을 반복하는 것은 불필요하고 많은 시간을 잡아먹게 된다.

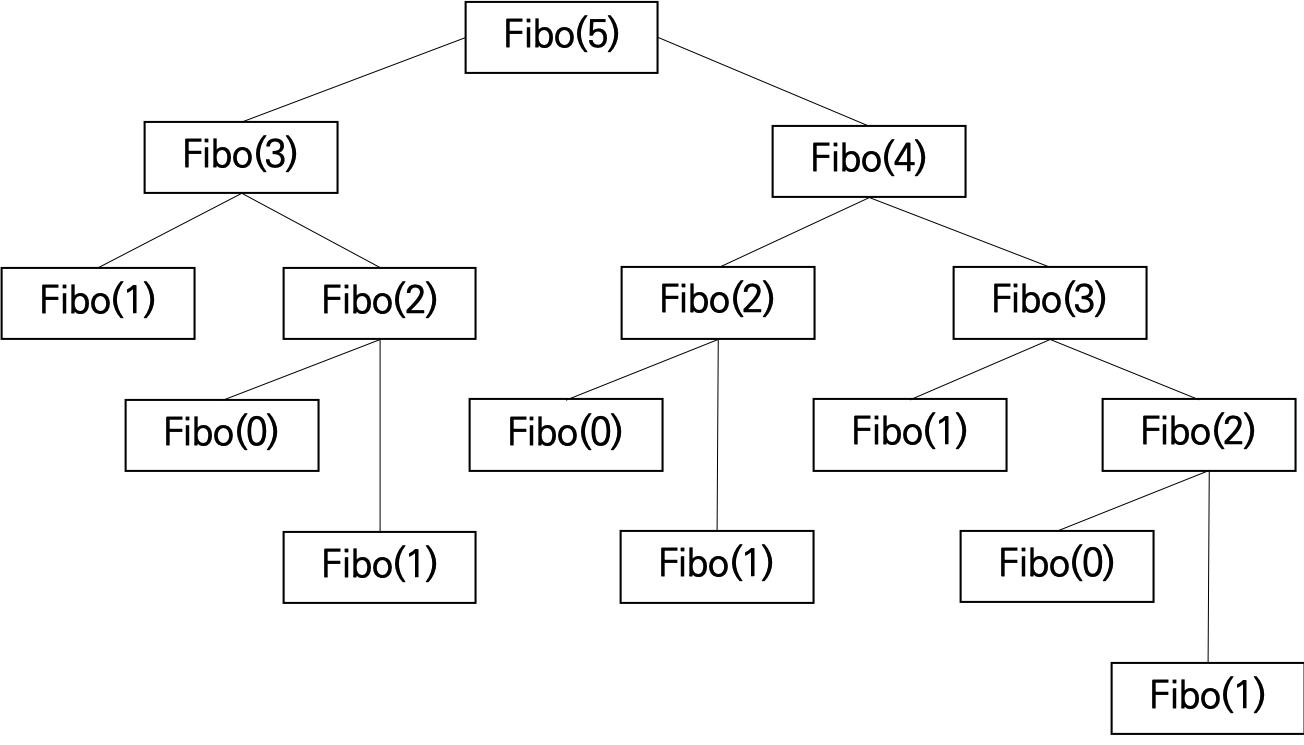
그래서, DP를 사용해야 한다.

DP를 사용하면 한번 구해놓은 값은 다시 구하지 않고 기존에 있는 저장된 값을 가져오게 된다. 이를 Memoization이라고 부른다. 불필요한 연산이 줄기 때문에 속도가 매우 향상된다.

# fibo(5)를 찾는다고 가정
fibo = [0 for _ in range(5)]
fibo[0] = 1
fibo[1] = 1

for i in range(2,5):
    fibo[i] = fibo[i-1] + fibo[i-2]

DP로 푼 피보나치 수열 문제는 전형적인 Bottom-Up 방식으로 푼 문제이다. Bottom-Up 방식이 무엇인지 이해하기 전에 반대되는 Top-Down 방식부터 이해하고 오자. **

문제를 푸는 방식 중에 Top-Down, Bottom-Up 방식이 있다. 피보나치 수열 문제를 재귀로 풀었을 때는 Top-Down 방식을 사용했다. Top-Down 큰 문제를 작은 sub-problem들로 풀어나가는 것이다. 재귀로 푼 해결책을 보면, Fibo(5)를 Fibo(4)와 Fibo(3)으로 쪼개서 계산하고 그 밑 값들도 비슷하게 진행한다.

반면에 DP의 Bottom-Up은 작은 문제들을 먼저 풀어서 큰 문제에 다가가는 것이다. 문제를 해결한 코드를 보면, fibo[0], fibo[1]값을 먼저 지정해주고 2부터 시작해서 n까지 서서히 답을 구하게 된다. 모든 sub-problem들에 대한 해결책을 저장하기 때문에 이 방법은 메모리를 더 많이 차지하게 된다.

그렇다면 항상 Bottom-Up 방식이 빠른가?

답부터 말하자면 아니다. Bottom-Up 방식이 피보나치 수열 문제에서는 재귀보다 빨랐지만, 모든 상황에서 빠른 것은 아니다. Bottom-Up 방식은 큰 문제까지 모든 sup-problem들을 계산해야 한다, 하지만 어떤 문제에서는 모든 sub-problem에 대한 해결책이 필요없을 수도 있다. Top-Down은 그 때 그 떄 필요한 sub-problem들만 호출해서 해결하기 때문에, 이러한 유형의 문제에서는 Top-Down 방식이 더 빠를 수도 있다.

DP의 종류들

DP로 풀 수 있는 가장 대표적인 문제 유형들:

Knapsack Problem(배낭문제)
LCS (Longest Common Sequence)
LIS (Longest Increasing Subsequence)
편집거리 (Edit distance)
행렬곱(Matrix Chain Multiplication)

이 유형들은 다음 Post들에서 다뤄볼 예정이다.